Flächenelemente
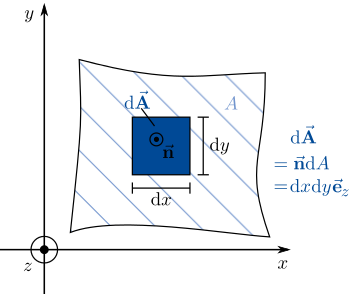
Im einfachsten Fall sind die zu bestimmenden Flächenelemente in kartesischen Koordinaten gegeben (wenn sie gegeben sind, müssen sie wohl nicht mehr bestimmt werden). Zunächst ist hier eine Integrationsfläche (was soll denn eine Integrationsfläche sein?) zu sehen, die sich in x-und y-Richtung ausbreitet. Ein infinitesimales Teilstück dieser Fläche muss dem zufolge auch in beide Richtungen ausgedehnt sein, um die gesamte Fläche beschreiben zu können (Argumentation unschlüssig). Eine Integration über 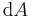 , kann dann auch als Integration über beide Wegelemente
, kann dann auch als Integration über beide Wegelemente 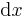 und
und 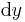 beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten sich die Fläche aus dem Produkt der Seiten x und y bestimmt.
beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten sich die Fläche aus dem Produkt der Seiten x und y bestimmt.
Es muss bei der vektoriellen Integration auch auf die Orientierung der Fläche geachtet werden. Dazu definiert man eine Flächennormale (man weiß nicht, was das ist), die orthogonal auf dem Flächenstück steht.
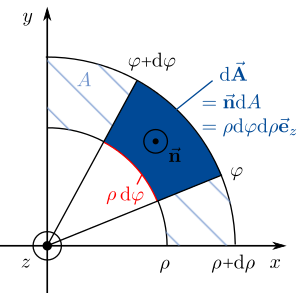
Wenn die Flächenelemente gekrümmt sind, dann müssen zur Berechnung der Flächenelemente (des Flächeninhalts?) so genannte Korrekturfaktoren eingeführt werden. Als Beispiel betrachtet man eine Kreisringfläche in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement beschreiben, so reicht es nicht aus einfach 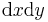 zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden (Argumentation unschlüssig). Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden.
dA = ??? Der Grafik hinzufügen!
zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden (Argumentation unschlüssig). Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden.
dA = ??? Der Grafik hinzufügen!
-> Reihenfolge der Richtungsangaben sollte korrespondieren!
Zur Bestimmung des Korrekturfaktors oder auch Metrikkoeffizienten betrachtet man nun ein Flächenelement des Kurvenstücks (vgl. Abbildung). Die Seitenlänge des Flächenelements entlang der r-Koordinate ist nicht gekrümmt und kann daher als 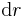 angenommen werden (Formulierung). Die
angenommen werden (Formulierung). Die  -Koordinate hängt auch von dem Radius r ab. Deshalb (unklar) ist das infinitesimale Flächenelement einer Kreisfläche
-Koordinate hängt auch von dem Radius r ab. Deshalb (unklar) ist das infinitesimale Flächenelement einer Kreisfläche 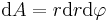 .
.