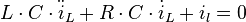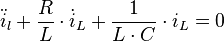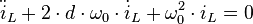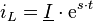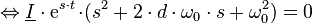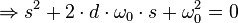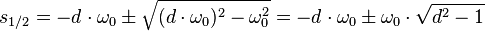Getb:Beispiel für eine DGL 2. Ordnung: Ein RLC-Schwingkreis

Lösung der homogenen DGL

Die zur schaltung dazugehörige homogene DGL lautet:

$L \cdot C \cdot \ddot i_L + R \cdot C \cdot \dot i_L + i_l = 0$

Teilen durch $LC$ liefert folgende Form:

$\ddot i_l + \frac{R}{L} \cdot \dot i_L + \frac{1}{L \cdot C} \cdot i_L = 0$

Nun werden einige wichtige Abkürzungen eingeführt:

• Kennkreisfrequenz: $\textstyle \omega_0 = \frac{1}{\sqrt{L \cdot C}}$

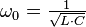
• Kennwiderstand: $\textstyle Z_0 = \sqrt{\frac{L}{C}}$

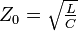
• Dämpfung: $\textstyle d = \frac{R}{2} \cdot \sqrt{\frac{C}{L}} = \frac{1}{2} \cdot \frac{R}{Z_0}$

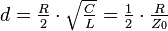
Damit lässt sich die homogene DGL kompakter darstellen:

$\ddot i_L + 2 \cdot d \cdot \omega_0 \cdot \dot i_L + \omega_{0}^2 \cdot i_L = 0$

Der Exponentialansatz lautet:

$i_L = \underline{I} \cdot \operatorname{e}^{s \cdot t}$

Es ist zu beachten, dass auch hier die möglicherweise komplexe Exponentialfunktion einheitenlos ist und für die komplexe Konstante (sowohl Real- als auch Imaginärteil) $[\underline{I}]=A$ gilt, da für die Einheit des Spulenstroms $[i_L] = A$ gelten muss.

Einsetzen des Ansatzes liefert die charakteristische Gleichung:

$s^2 \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} + 2 \cdot d \cdot \omega_0 \cdot s \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} + \omega_{0}^2 \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} = 0$

$\Leftrightarrow \underline{I} \cdot \operatorname{e}^{s \cdot t} \cdot (s^2 + 2 \cdot d \cdot \omega_0 \cdot s + \omega_{0}^2 ) = 0$

$\Rightarrow s^2 + 2 \cdot d \cdot \omega_0 \cdot s + \omega_{0}^2 = 0$

Die Koeffizienten der charakteristischen Gleichung sind also identisch mit den Koeffizienten der homogenen DGL, wenn diese von der normalisierten Form einer linearen DGL ist. Die Lösung der charakteristischen Gleichung ergibt die Eigenwerte:

$s_{1/2} = -d \cdot \omega_0 \pm \sqrt{(d \cdot \omega_0)^2 - \omega_{0}^2} = -d \cdot \omega_0 \pm \omega_0 \cdot \sqrt{d^2 -1}$

Dies führt zu den drei verschiedenen Lösungsfällen:

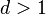1. $d > 1$ (starke Dämpfung) 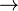$\rightarrow$ zwei verschiedene, reelle Eigenwerte
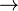2. $d = 1$ (aperiodischer Grenzfall) $\rightarrow$ zwei gleiche, reelle Eigenwerte
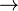3. $d < 1$ (schwache Dämpfung) $\rightarrow$ zwei zueinander konjugiert komplexe Eigenwerte