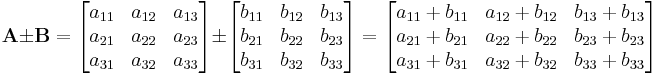Einfache Rechenoperationen mit Matrizen
|
Dieser Artikel befindet sich noch im Aufbau. |
Bei der Rechnung mit Matrizen meist die Gesetzmäßigkeiten aus der Vektorrechnung. Dies ist auch deshalb plausibel, weil ein Vektor auch als Spezielfall einer Matrix mit nur einer Spalte aufgefasst werden kann. Lediglich bei der Multiplikation von Matrizen unterscheidet sich das Vorgehen.
Inhaltsverzeichnis
Addition und Subtraktion von Matrizen
Sollen zwei Matrizen addiert oder subtrahiert werden, so müssen diese die gleiche Anzahl an Zeilen und Spalten haben. Formal formuliert können also nur dann zwei 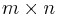 Matrizen addiert oder subtrahiert werden, wenn
Matrizen addiert oder subtrahiert werden, wenn 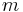 und
und 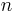 jeweils gleich sind. Die Berechnung der Summe beziehungsweise Differenz erfolgt durch die Addition beziehungsweise Subtraktion der jeweils zusammengehörigen Einträge.
jeweils gleich sind. Die Berechnung der Summe beziehungsweise Differenz erfolgt durch die Addition beziehungsweise Subtraktion der jeweils zusammengehörigen Einträge.
Beispiel für zwei  -Matrizen:
-Matrizen:
Die Reihenfolge, in der die Rechnung ausgeführt wird, spielt damit keine Rolle. Damit gilt das Kommutativgesetz, das heißt 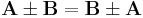 .
.
Multiplikation von Matrizen mit einem Skalar
Division von Matrizen
Ähnlich wie bei der Vektorrechnung ist die Division von Matrizen nicht definiert. Jedoch existiert der Begriff der Inversen einer Matrix, mit dessen Hilfe eine Division auf eine Multiplikation zurückgeführt werden kann.