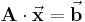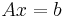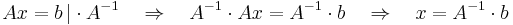Allgemeine Formulierung linearer Gleichungssysteme
|
Dieser Artikel befindet sich noch im Aufbau. |
Im Rahmen der Einführung zu linearen Gleichungssystemen wurde bereits beschrieben, dass lineare Gleichungssysteme in Matrixschreibweise allgemein wie folgt angegeben werden können:
Dabei werden die nachstehenden Bezeichnungen verwendet:
 : Koeffizientenmatrix
: Koeffizientenmatrix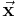 : Lösungs- oder Variablenvektor (enthält die gesuchten Variablen)
: Lösungs- oder Variablenvektor (enthält die gesuchten Variablen) : Konstantenvektor oder „rechte Seite“
: Konstantenvektor oder „rechte Seite“
Dabei handelt es sich um eine spezielle Schreibweise eines Systems (also mehrerer zusammengehöriger) linearer Gleichungen. Im allgemeinsten Fall liegt ein System aus 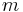 linearen Gleichungen mit
linearen Gleichungen mit 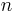 unbekannten Variablen
unbekannten Variablen 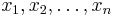 vor:
vor:
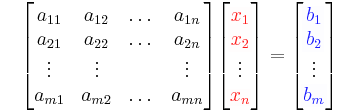
In Matrixschreibweise kann das lineare Gleichungssystem wie folgt angegeben werden:
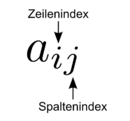
Die Elemente (Einträge) der 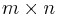 -Matrix
-Matrix  werden also mit
werden also mit 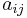 bezeichnet, wobei
bezeichnet, wobei 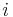 die Zeile und
die Zeile und 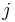 die Spalte des betrachteten Elements angibt (vgl. Abbildung).
die Spalte des betrachteten Elements angibt (vgl. Abbildung).
Aufgrund der Tatsache, dass zur Bestimmung von 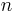 unbekannten Größen auch (mindestens)
unbekannten Größen auch (mindestens) 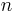 linear unabhängige Gleichungen erforderlich sind, handelt es sich bei
linear unabhängige Gleichungen erforderlich sind, handelt es sich bei  häufig um eine quadratische Matrix. In diesem Fall gilt
häufig um eine quadratische Matrix. In diesem Fall gilt 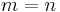 und die Anzahl der Zeilen und Spalten ist folglich identisch (
und die Anzahl der Zeilen und Spalten ist folglich identisch (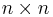 -Matrix).
-Matrix).
Lösung linearer Gleichungssysteme
Zur Lösung linearer Gleichungssysteme, also zur Bestimmung der Größen 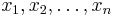 beziehungsweise des Vektors
beziehungsweise des Vektors 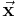 , existiert eine Vielzahl von Verfahren. Handelt es sich bei
, existiert eine Vielzahl von Verfahren. Handelt es sich bei  um eine quadratische Matrix, so kann beispielsweise die Cramersche Regel verwendet werden. Ausgangspunkt für die weiteren Betrachtungen ist zunächst eine Gleichung mit ausschließlich skalaren Größen
um eine quadratische Matrix, so kann beispielsweise die Cramersche Regel verwendet werden. Ausgangspunkt für die weiteren Betrachtungen ist zunächst eine Gleichung mit ausschließlich skalaren Größen 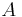 ,
,  und
und 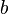 :
:
Um in diesem Fall die Unbekannte  zu bestimmen, genügt eine Multiplikation der Gleichung mit
zu bestimmen, genügt eine Multiplikation der Gleichung mit 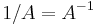 :
:
Inverse. Determinante. Multiplikation. Idee: Einfache Rechenoperationen mit Matrizen. Anzahl der Lösungen.
To-Do:
- Bild zur Indizierung oben rechts einfügen
- Zusammenhang zur Multiplikation von Matrizen
- Hinweis zur Anzahl der Zeilen und Spalten
- Übergang zu quadratischen Matrizen
- Lösung solcher Gleichungssysteme und entsprechende Bedingungen