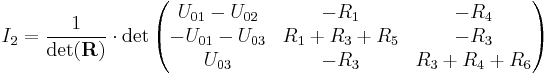Cramersche Regel

To-do:

Einleitung etwas plausibler (es gibt doch genügend Beispiele)
Formulierungen überarbeiten (insbes. fett)
Restriktionen angeben
Bedeutung der Elemente in den Formeln der Cramerschen Regel sind schlecht dargestellt

Das Invertieren einer Matrix ist meist sehr aufwendig. Deswegen kann man die Cramersche Regel nutzen, um bei Gleichungssystemen der Form:

\mathbf{A}\cdot\vec{\mathbf{x}}=\vec{\mathbf{b}}

den Lösungsvektor $\vec{\mathbf{x}}$ zu bestimmen.

Die Cramersche Regel oder auch das Determinantenverfahren genannt, lautet:

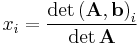
$x_i=\frac{\det{(\mathbf{A,b})}_i}{\det{\mathbf{A}}}$

Dabei ersetzt man zunächst die Spalte mit dem Spaltenvektor 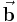$\vec{\mathbf{b}}$ in der Matrix, deren Lösung man haben möchte. Soll berechnet werden welcher Wert an der Stelle 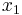$x_1$ im Lösungsvektor steht, muss man die erste Spalte der Matrix mit 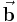$\vec{\mathbf{b}}$ ersetzen. Dann müssen die Determinaten der so neu gewonnen Matrix und der Matrix 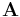$\mathbf{A}$ bestimmt werden.

Um alle Werte des Lösungsvektors zu bekommen, muss man das Verfahren mehrfach anwenden.

Beispiel: Anwendung der Cramersche Regel

Durch eine Knotenanalyse ergibt sich folgendes lineares Gleichungssystem:

\begin{pmatrix} R_1+R_2+R_4 & -R_1 & -R_4 \\ -R_1 & R_1+R_3+R_5 & -R_3 \\ -R_4 & -R_3 & R_3+R_4+R_6 \end{pmatrix} \cdot \begin{pmatrix} I_2\\ I_5\\ I_6 \end{pmatrix} = \begin{pmatrix} U_{01}-U_{02}\\ -U_{01}-U_{03}\\ U_{03} \end{pmatrix}

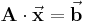
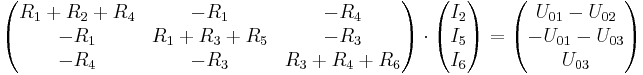
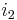Nun soll das erste Element des Lösungsvektors, also $i_2$ bestimmt werden. Dazu muss also der Quellvektor in die erste Spalte der Koeffizientenmatrix gesetzt werden.: