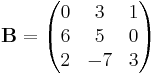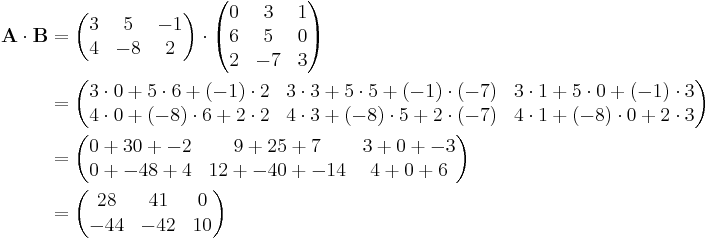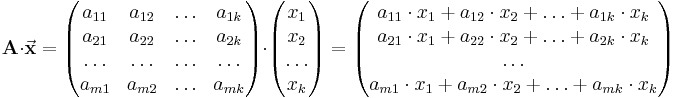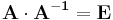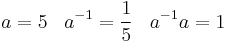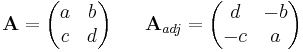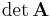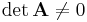Lineare Gleichungssysteme
Eine Zusammenschaltung von verschiedenen aktiven oder passiven, linearen Zweipolen heißt Lineares Netzwerk. Es lässt sich durch lineare Gleichungssysteme beschreiben.
Um solch ein lineares Gleichungssystem aufzustellen, kann man die Kirchhoffschen Gesetze, also Maschen-, und Knotengleichungen verwenden. Dementsprechend wird eine Maschenanalyse angewandt, wenn die Ströme eines Netzwerks in einigen oder allen Zweigen gesucht sind. Sind die Spannungen gesucht, verwendet man die Knotenanalyse. Die Gleichungssysteme erhalten dabei folgende Formen:
oder
oder in allgemeiner Form:
Matrizen werden hier, um sie von anderen, zum Beispiel skalaren Größen zu unterscheiden fett gedruckt. Dabei können Vektoren als Sonderfall von Matrizen aufgefasst werden, die nur eine Spalte besitzen. Ebenfalls sollte beachtet werden, dass hier die gesuchten Größen bei diesen Gleichungen auf der linken Seite stehen, also auf der selben Seite wie die Widerstands- oder Leitwertmatrix.
Inhaltsverzeichnis
Einzelteile des Linearen Gleichungssystems
Koeffizientenmatrix
Die Koeffizientenmatrix, oben auch Widerstands-, oder Leitwertmatrix genannt, enthält alle in den Maschen vorkommenden Widerstände oder Leitwerte. Sie ist aus m Zeilen und n Spalten aufgebaut ((m x n )-Matrix). Dabei hat sie immer folgende Form:
Die Elemente der Matrix  sollen hier nur rein reelwertig angenommen werden. Man beachte die Reihenfolge, sodass i der Zeilenindex und j der Spaltenindex ist.
sollen hier nur rein reelwertig angenommen werden. Man beachte die Reihenfolge, sodass i der Zeilenindex und j der Spaltenindex ist.
Hier werden nur quadratische Koeffizientenmatrixen angenommen, da sie zur Maschen-, oder Knotenanalyse verwendet werden können. Da uns dort die unbekannten Größen interessieren, brauchen wir genausoviele linear unbahängige Gleichungen wie Unbekannte, um das System lösen zu können. In anderen Fällen wäre es sonst über- oder unterbestimmt.
Die Spaltenvektoren
Die Spaltenvektoren  und
und 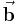 entsprechen in den hier betrachteten Fällen immer Strömen und Spannungen. Sie haben folgende Form:
entsprechen in den hier betrachteten Fällen immer Strömen und Spannungen. Sie haben folgende Form:
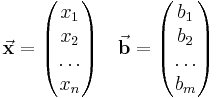
Dabei ist zu beachten das der  -Vektor immer die gesuchten Größen enthält.
-Vektor immer die gesuchten Größen enthält.
Matrizenrechnung
Multiplikation zweier Matrizen
Möchte man zwei Matrizen multiplizieren, gibt es ein bestimmtes Rechenschema, dass eingehalten werden muss. Dabei ist es wichtig, dass die Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix übereinstimmt. Dies impliziert auch, dass die Matrizenmultiplikation nicht kommuntativ ist, also die Matrizen in einer Rechnung auf keinen Fall getauscht werden dürfen.
Um nun das erste Element der neuen Matrix zu berechnen, muss man das erste Element der ersten Zeile der ersten Matrix mit dem ersten Element der ersten Spalte der zweiten Matrix multiplizieren und anschließend das zweite Element der ersten Zeile der ersten Matrix mit dem zweiten Element der ersten Spalte der zweiten Matrix multipliziert und die Ergebnisse der Multiplikationen aufaddiert werden. Dies führt man solange durch, bis das letzte Element der ersten Zeile der ersten Matrix und das letzte Element der ersten Spalte der zweiten Matrix erreicht ist. Daraus folgt auch, die Gleichheit der Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix, die vorher schon gefordert wurde.
Einfacher wird es wenn man sich zwei kleine Matrizen, als Beispiel 2 2x2-Matrizen anschaut. Dort lautet das Rechenschema:
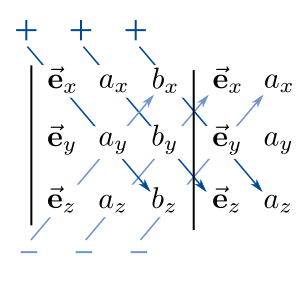
Eine weitere Merkhilfe bietet das, in der Abbildung an einer 2x2-Matrix gezeigte Falk-Schema. Hier wird die Matrix A links von der zu berechnenden Matrix aufgetragen und die Matrix B über der zu berechnenden Matrix eingezeichnet. Um ein Element in der gesuchten Matrix zu erhalten, betrachtet man nun die Elemente, die bei der Matrix A in der selben Zeile stehen und bei der Matrix B in der selben Spalte, also entlang der eingezeichneten Linien. Nun muss man nur noch das Skalarprodukt aus dem Zeilenvektor von der Matrix A und dem Spaltenvektor aus der Matrix B gebildet werden, um das Element zu berechnen.
In diesem Beispiel sind die zwei Matrizen A und B gegeben:
wie man sieht sind die beiden Matrizen A und B nicht gleich dimensioniert. Allerdings stimmt die Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix überein. Also sind diese beiden Matrizen multiplizierbar. Als Formel kann man sich merken, dass das Produkt der Matrizen die selbe Spaltenanzahl, wie die erste Matrix und die selbe Zeilenanzahl, wie die zweite Matrix besitzen muss. Nutzt man nun die oben genannte Form ergibt sich: |
Multiplikation von Matrix und Vektor
Vektoren können als Sonderform von Matrizen betrachtet werden, die nur eine Spalte besitzen. Möchte man eine Matrix mit einen Vektor multiplizieren muss also immer zuerst die Matrix stehen und anschließend erst der Vektor und die Zeilenanzahl der Matrix muss der Spaltenanzahl des Vektors entsprechen:
Einheitsmatrix und Inverse
Der Lösungsvektor x steht in der oben beschriebenen Form immer mit der Koeffizientenmatrix auf einer Seite. Nun soll der Lösungsvektor durch umstellen der Gleichung aber bestimmt werden. Da man aber niemals durch einen Vektor teilen darf, muss man sich einem anderen mathematischen Hilfsmittel bedienen, der Inverse der Matrix 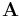 .
.
Um die Inverse einer Matrix zu verstehen, betrachtet man zunächst eine andere besondere quadratische Matrix, die Einheitsmatrix 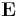 . In manchen Büchern wird sie auch mit einer
. In manchen Büchern wird sie auch mit einer 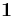 dargestellt.
Sie hat folgende Form:
dargestellt.
Sie hat folgende Form:
Dabei ist die Matrix, die Inverse und die Einehitsmatrix in folgender Form verknüpft:
Dies gilt allerdings nur unter der Vorraussetzung, dass die Inverse von A also 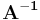 existiert. Dies ist dann der Fall, wenn die Determinante nicht 0 ist.
Um also den Lösungsvektor x zu bestimmen,muss die Inverse existieren.
existiert. Dies ist dann der Fall, wenn die Determinante nicht 0 ist.
Um also den Lösungsvektor x zu bestimmen,muss die Inverse existieren.
Analog zu der Einheitsmatrix, kann man in den reellen Zahlen die 1 als Eins-Element betrachten. Dort funktioniert dies auf ähnliche Weise mit allen rationalen Zahlen. Es gibt zu jeder Zahl einen Bruch, der mit der Zahl multipliziert wieder 1 ergibt:
Um nun die Inverse einer Matrix zu bestimmen benötigt man folgende Rechenvorschrift:
Hierbei wird auch deutlich, dass die Determinante der Matrix nicht 0 sein darf, wenn die Inverse der Matrix existieren soll. Da sonst bei Bestimmung der Inverse durch 0 geteilt werden müsste und so einen unbestimmten Ausdruck ergäbe.
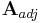 heißt die Adjunkte von
heißt die Adjunkte von 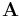 . Für eine 2x2-Matrix, die in dieser Veranstaltung vollkommen ausreicht, ergibt sich dafür folgende Form:
. Für eine 2x2-Matrix, die in dieser Veranstaltung vollkommen ausreicht, ergibt sich dafür folgende Form:
Determinante einer Matrix
Eine quadratische Matrix 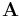 wird auf eindeutige Weise einer bestimmten Zahl zugeordnet, diese Zahl heißt Determinante der Matrix, oder in mathematischer Schreibweise:
wird auf eindeutige Weise einer bestimmten Zahl zugeordnet, diese Zahl heißt Determinante der Matrix, oder in mathematischer Schreibweise:
Die Determinante, ist dabei ein Maß für die Lösbarkeit eines linearen Gleichungssystems. Es gilt, wenn die Determinante ungleich null ist, also:
ist das System linear unabhängig und damit eindeutig lösbar. Umgekehrt gilt ebenso: Ist die Determinate gleich 0, gibt es unendlich viele verschiedene Lösungen und das System damit auch nicht linear unabhängig ist.
= Berechnung der Determinante
In diesem Abschnitt sollen zwei Lösungsverfahren, zur Bestimmung der Determinante besprochen werden.
a)
Das erste Lösungsverfahren, das Enwickeln der Matrix nach einer beliebigen Zeile oder Spalte ist ein Verfahren das allgemein gilt und immer verwendet werden kann.
b) Das zweite Verfahren die Regel von Sarrus, gilt nur bei 3x3-Matrizen oder kleiner. Es ist allerdings viel weniger aufwendig.
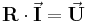
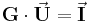
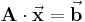

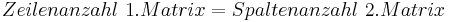
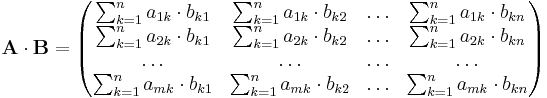
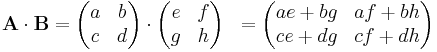
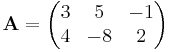 und
und