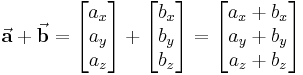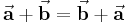Einfache Rechenoperationen mit Vektoren

Addition und Subtraktion von Vektoren

Vektoraddition und -subtraktion

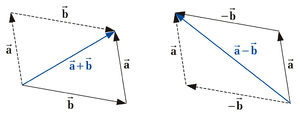
Vektoren lassen sich sowohl graphisch als auch rechnerisch addieren. Bei der grafischen Addition wird einer der Vektoren parallel verschoben, so dass sein Anfang an der Spitze des zweiten Pfeils liegt (die Vektoren werden also sozusagen aneinandergereiht). Der resultierende Vektor wird als Summenvektor bezeichnet und zeigt vom Anfangspunkt des einen Vektors zur Spitze des parallel verschobenen Vektors (siehe Abbildung). Zur mathematischen Bestimmung der beiden Vektoren werden die einzelnen Komponenten addiert:

$\vec{\textbf{a}} + \vec{\textbf{b}} = \begin{bmatrix} a_x\\a_y\\a_z \end{bmatrix} + \begin{bmatrix} b_x\\b_y\\b_z \end{bmatrix} = \begin{bmatrix} a_x+b_x\\a_y+b_y\\a_z+b_z \end{bmatrix}$

Sowohl anhand der grafischen Addition — es spielt offensichtlich keine Rolle welcher der beiden Vektoren an die Spitze des anderen verschoben wird — als auch anhand der rechnerischen Bestimmung des Summenvektors wird deutlich, dass die Vektoraddition dem Kommutativgesetz genügt. Folglich gilt:

$\vec{\textbf{a}}+\vec{\textbf{b}} = \vec{\textbf{b}}+\vec{\textbf{a}}$

Bei der Subtraktion zweier Vektoren wird der resultierende Vektor als Differenzvektor bezeichnet. Zur graphischen Bestimmung des Differenzvektors 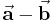$\vec{\textbf{a}}-\vec{\textbf{b}}$ lässt sich ausnutzen, dass 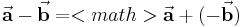$\vec{\textbf{a}}-\vec{\textbf{b}} = <math>\vec{\textbf{a}}+(-\vec{\textbf{b}})$ gilt.