Erweiterung der Integralrechnung:Übersicht: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
|- | |- | ||
| − | |[[#Das Linienintegral|Das Linienintegral]] | + | |[[#Das Linienintegral|center|Das Linienintegral]] |
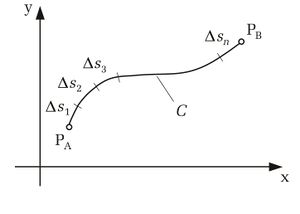
Das '''Linien-''' oder '''Kurvenintegral''', erstreckt sich entlang einer Kontur C, z. B. von einem Anfangspunkt <math> P_A </math> bis zu einem Endpunkt <math> P_B </math>.Ist der Integrationsweg ''C'' eine geschlossene Kontur, d. h. Anfangs- und Endpunkt fallen zusammen (<math> P_A = P_B </math>), dann wird das Linienintegral als '''Ringintegral''' bezeichnet und das Integralzeichen wird mit einem Ring dargestellt. | Das '''Linien-''' oder '''Kurvenintegral''', erstreckt sich entlang einer Kontur C, z. B. von einem Anfangspunkt <math> P_A </math> bis zu einem Endpunkt <math> P_B </math>.Ist der Integrationsweg ''C'' eine geschlossene Kontur, d. h. Anfangs- und Endpunkt fallen zusammen (<math> P_A = P_B </math>), dann wird das Linienintegral als '''Ringintegral''' bezeichnet und das Integralzeichen wird mit einem Ring dargestellt. | ||
| Zeile 14: | Zeile 14: | ||
|- | |- | ||
| − | |[[#Das Flächenintegral|Das Flächenintegral]] | + | |[[#Das Flächenintegral|center|Das Flächenintegral]] |
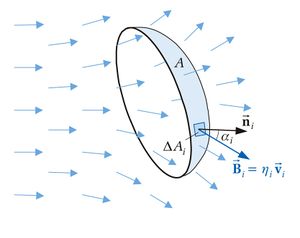
Das '''Flächenintegral''' oder '''Oberflächenintegral''' beschreibt eine Integration über eine ebene oder gekrümmte Fläche. Im Gegensatz zum Linienintegral wird hier also kein eindimensionales Intervall betrachtet, sondern eine Schachtelung von zwei Integralen mit verschiedenen Integrationsvariablen, beispielsweise <math>x,y</math>, die die Fläche <math>\text{A}</math> über die integriert werden soll, aufspannen. Ist die Fläche geschlossen, gilt also <math> (x_1=x_2), (y_1=y_2)</math> spricht man von einem '''Hüllflächenintegral''' und verwendet wie beim Ringintegral ein Ring im Integralzeichen, um dies darzustellen. | Das '''Flächenintegral''' oder '''Oberflächenintegral''' beschreibt eine Integration über eine ebene oder gekrümmte Fläche. Im Gegensatz zum Linienintegral wird hier also kein eindimensionales Intervall betrachtet, sondern eine Schachtelung von zwei Integralen mit verschiedenen Integrationsvariablen, beispielsweise <math>x,y</math>, die die Fläche <math>\text{A}</math> über die integriert werden soll, aufspannen. Ist die Fläche geschlossen, gilt also <math> (x_1=x_2), (y_1=y_2)</math> spricht man von einem '''Hüllflächenintegral''' und verwendet wie beim Ringintegral ein Ring im Integralzeichen, um dies darzustellen. | ||
| Zeile 23: | Zeile 23: | ||
|- | |- | ||
| − | |[[#Das Volumenintegral|Das Volumenintegral]] | + | |[[#Das Volumenintegral|center|Das Volumenintegral]] |
Das '''Volumen-''' oder '''Dreifachintegral''' ist eine Funktion, die dreimal hintereinander integriert wird, jeweils über eine Richtung eines dreidimensionalen Raumes, dabei wird das Volumen <math>\text{V}</math> aufgespannt. | Das '''Volumen-''' oder '''Dreifachintegral''' ist eine Funktion, die dreimal hintereinander integriert wird, jeweils über eine Richtung eines dreidimensionalen Raumes, dabei wird das Volumen <math>\text{V}</math> aufgespannt. | ||
| Zeile 30: | Zeile 30: | ||
|<center><math>\int\limits_V \rho \cdot \mathrm{d}\vec{\textbf{V}}</math><br> | |<center><math>\int\limits_V \rho \cdot \mathrm{d}\vec{\textbf{V}}</math><br> | ||
| − | |[[Image:Erweiterung_der_integralrechnung_Fluss.jpg|miniatur|]] | + | |[[Image:Erweiterung_der_integralrechnung_Fluss.jpg|miniatur|center]] |
|} | |} | ||
Version vom 24. Februar 2012, 11:38 Uhr
| center|Das Linienintegral
Das Linien- oder Kurvenintegral, erstreckt sich entlang einer Kontur C, z. B. von einem Anfangspunkt |
|
|
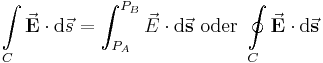
| center|Das Flächenintegral
Das Flächenintegral oder Oberflächenintegral beschreibt eine Integration über eine ebene oder gekrümmte Fläche. Im Gegensatz zum Linienintegral wird hier also kein eindimensionales Intervall betrachtet, sondern eine Schachtelung von zwei Integralen mit verschiedenen Integrationsvariablen, beispielsweise |
|
|
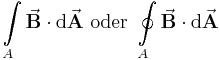
| center|Das Volumenintegral
Das Volumen- oder Dreifachintegral ist eine Funktion, die dreimal hintereinander integriert wird, jeweils über eine Richtung eines dreidimensionalen Raumes, dabei wird das Volumen
|
 |
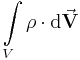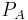bis zu einem Endpunkt 
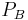.Ist der Integrationsweg C eine geschlossene Kontur, d. h. Anfangs- und Endpunkt fallen zusammen (
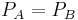), dann wird das Linienintegral als Ringintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
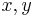, die die Fläche 
über die integriert werden soll, aufspannen. Ist die Fläche geschlossen, gilt also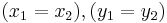 
spricht man von einem Hüllflächenintegral und verwendet wie beim Ringintegral ein Ring im Integralzeichen, um dies darzustellen.
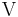aufgespannt.
