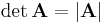Determinante: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
Neben der Verwendung des Operators <math>\det</math> werden also auch häufig einfach Betragsstriche verwendet. | Neben der Verwendung des Operators <math>\det</math> werden also auch häufig einfach Betragsstriche verwendet. | ||
| − | Es lässt sich zeigen, dass ein lineares Gleichungssystem genau dann eindeutig lösbar ist, wenn die Determinante der Koeffizientenmatrix <math>\textbf{A}</math> ungleich Null ist (es muss also <math>\det\textbf{A} \neq 0</math> gelten). Ist dies nicht der Fall, so besitzt das Gleichungssystem unendlich viele Lösungen oder gar keine Lösung. Dies ist der Fall, wenn die Zeilen von <math>\textbf{A}</math> linear abhängig (also ''nicht'' linear unabhängig) sind. Wurde das lineare Gleichungssystem im Rahmen einer Knoten- und Maschenanalyse ermittelt, so ist dieses | + | Es lässt sich zeigen, dass ein lineares Gleichungssystem genau dann eindeutig lösbar ist, wenn die Determinante der Koeffizientenmatrix <math>\textbf{A}</math> ungleich Null ist (es muss also <math>\det\textbf{A} \neq 0</math> gelten). Ist dies nicht der Fall, so besitzt das Gleichungssystem unendlich viele Lösungen oder gar keine Lösung. Dies ist der Fall, wenn die Zeilen von <math>\textbf{A}</math> linear abhängig (also ''nicht'' linear unabhängig) sind. Wurde das lineare Gleichungssystem im Rahmen einer Knoten- und Maschenanalyse ermittelt, so ist dieses normalerweise eindeutig lösbar. |
==Determinanten zweiter Ordnung== | ==Determinanten zweiter Ordnung== | ||
Version vom 26. November 2012, 20:30 Uhr
|
|
Dieser Artikel befindet sich noch im Aufbau. |
Unter einer Determinante versteht man eine Zahl, die auf eindeutige Weise einer quadratischen Matrix zugeordnet werden kann. Die Zahl sagt etwas aus (determinieren = bestimmen/festlegen) über die Lösbarkeit eines linearen Gleichungssystems der Form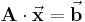 
und spielt eine wichtige Rolle bei der Bestimmung der zugehörigen Lösung (vgl. Cramersche Regel). Die Ordnung einer Determinante entspricht der Anzahl der Zeilen (da sich der Begriff auf quadratische Matrizen bezieht stimmt diese mit der Anzahl der Spalten überein) der betrachteten Matrix. Ist die Determinante einer Matrix 
zu bestimmen, so wird dies durch die folgenden Schreibweisen dargestellt:
Neben der Verwendung des Operators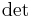 
werden also auch häufig einfach Betragsstriche verwendet.
Es lässt sich zeigen, dass ein lineares Gleichungssystem genau dann eindeutig lösbar ist, wenn die Determinante der Koeffizientenmatrix ungleich Null ist (es muss also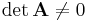 
gelten). Ist dies nicht der Fall, so besitzt das Gleichungssystem unendlich viele Lösungen oder gar keine Lösung. Dies ist der Fall, wenn die Zeilen von linear abhängig (also nicht linear unabhängig) sind. Wurde das lineare Gleichungssystem im Rahmen einer Knoten- und Maschenanalyse ermittelt, so ist dieses normalerweise eindeutig lösbar.
