Cramersche Regel: Unterschied zwischen den Versionen
Aus GET A
| Zeile 2: | Zeile 2: | ||
{{Navigation|before=[[Determinante einer quadratischen Matrix]]|overview=[[Lineare Gleichungssysteme:Übersicht|Lineare Gleichungssysteme]]|next=[[Vektorrechnung:Übersicht|Übersicht Vektorrechnung]]}} | {{Navigation|before=[[Determinante einer quadratischen Matrix]]|overview=[[Lineare Gleichungssysteme:Übersicht|Lineare Gleichungssysteme]]|next=[[Vektorrechnung:Übersicht|Übersicht Vektorrechnung]]}} | ||
| − | Die Cramersche Regel wird auch als '''Determinantenverfahren''' bezeichnet und stellt eine Methode zur Lösung linearer Gleichungssysteme dar. Voraussetzung für die Anwendung des Verfahrens ist, dass die [[Koeffizientenmatrix]] <math>\textbf{A}</math> quadratisch ist und ihre [[Determinante]] <math>\det\textbf{A}</math> nicht verschwindet (<math>\det\textbf{A} \neq 0</math>). Solche Gleichungssysteme ergeben sich beispielsweise im Rahmen einer Knoten- oder Maschenanalyse. | + | Die Cramersche Regel wird auch als '''Determinantenverfahren''' bezeichnet und stellt eine Methode zur Lösung [[linearer Gleichungssysteme|Einführung zu linearen Gleichungssystemen]] dar. Voraussetzung für die Anwendung des Verfahrens ist, dass die [[Koeffizientenmatrix]] <math>\textbf{A}</math> quadratisch ist und ihre [[Determinante]] <math>\det\textbf{A}</math> nicht verschwindet (<math>\det\textbf{A} \neq 0</math>). Solche Gleichungssysteme ergeben sich beispielsweise im Rahmen einer Knoten- oder Maschenanalyse. |
[[Kategorie:Artikel]] | [[Kategorie:Artikel]] | ||
[[Kategorie:Feedback]] | [[Kategorie:Feedback]] | ||
Version vom 26. November 2012, 14:52 Uhr
|
|
Dieser Artikel befindet sich noch im Aufbau. |
| ← Zurück: Determinante einer quadratischen Matrix | Übersicht: Lineare Gleichungssysteme | Vorwärts: Übersicht Vektorrechnung → |
Die Cramersche Regel wird auch als Determinantenverfahren bezeichnet und stellt eine Methode zur Lösung Einführung zu linearen Gleichungssystemen dar. Voraussetzung für die Anwendung des Verfahrens ist, dass die Koeffizientenmatrix 
quadratisch ist und ihre Determinante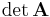 
nicht verschwindet (
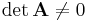). Solche Gleichungssysteme ergeben sich beispielsweise im Rahmen einer Knoten- oder Maschenanalyse.
