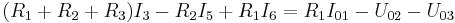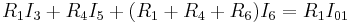Einführung zu linearen Gleichungssystemen: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
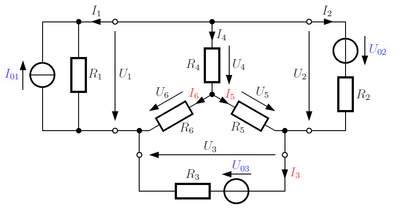
[[Datei:Netzwerk.png||miniatur|400px|Ein Netzwerk aus linearen Zweipolen]] | [[Datei:Netzwerk.png||miniatur|400px|Ein Netzwerk aus linearen Zweipolen]] | ||
| − | Im Rahmen der Lehrveranstaltung werden lineare Gleichungssysteme (kurz '''LGS''') zur Beschreibung linearer Netzwerke benötigt. Darunter versteht man eine ''beliebige'' Zusammenschaltung aktiver (z. B. Strom- und Spannungsquellen) und passiver (z. B. ohmsche Widerstände) linearer [[Zweipole]]. Ausgangspunkt zur Bestimmung solcher Gleichungssysteme sind in der Regel die Kirchhoffschen Gesetze, also Maschen- und Knotengleichungen | + | Im Rahmen der Lehrveranstaltung werden lineare Gleichungssysteme (kurz '''LGS''') zur Beschreibung linearer Netzwerke benötigt. Darunter versteht man eine ''beliebige'' Zusammenschaltung aktiver (z. B. Strom- und Spannungsquellen) und passiver (z. B. ohmsche Widerstände) linearer [[Zweipole]]. Ausgangspunkt zur Bestimmung solcher Gleichungssysteme sind in der Regel die Kirchhoffschen Gesetze, also Maschen- und Knotengleichungen. Möchte man nämlich <math>z</math> unbekannte Größen (z. B. Spannungen) in einem Netzwerk bestimmen, so sind hierzu auch (mindestens) <math>z</math> [[linear unabhängige]] Gleichungen erforderlich. Die Verknüpfung dieser Gleichungen zu einem Gleichungssystem widerspiegelt die Tatsache, dass im Allgemeinen jeder Zweipol die Zweigspannungen und -ströme eines Netzwerks beeinflusst. |
Durch eine systematische Vorgehensweise – nämlich der '''Knoten- und Maschenanalyse''' – lassen sich lineare Gleichungssysteme aufstellen, die eine gezielte Bestimmung von unbekannten Zweigspannungen beziehungsweise -strömen in einem Netzwerk ermöglichen. Im Rahmen einer Maschenanalyse könnten zum Beispiel die folgenden drei Gleichungen ermittelt worden sein: | Durch eine systematische Vorgehensweise – nämlich der '''Knoten- und Maschenanalyse''' – lassen sich lineare Gleichungssysteme aufstellen, die eine gezielte Bestimmung von unbekannten Zweigspannungen beziehungsweise -strömen in einem Netzwerk ermöglichen. Im Rahmen einer Maschenanalyse könnten zum Beispiel die folgenden drei Gleichungen ermittelt worden sein: | ||
Version vom 22. November 2012, 12:14 Uhr
|
|
Dieser Artikel befindet sich noch im Aufbau. |
| ← Zurück: XXX | Übersicht: XXX | Vorwärts: XXX → |
Im Rahmen der Lehrveranstaltung werden lineare Gleichungssysteme (kurz LGS) zur Beschreibung linearer Netzwerke benötigt. Darunter versteht man eine beliebige Zusammenschaltung aktiver (z. B. Strom- und Spannungsquellen) und passiver (z. B. ohmsche Widerstände) linearer Zweipole. Ausgangspunkt zur Bestimmung solcher Gleichungssysteme sind in der Regel die Kirchhoffschen Gesetze, also Maschen- und Knotengleichungen. Möchte man nämlich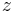 
unbekannte Größen (z. B. Spannungen) in einem Netzwerk bestimmen, so sind hierzu auch (mindestens) 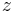linear unabhängige Gleichungen erforderlich. Die Verknüpfung dieser Gleichungen zu einem Gleichungssystem widerspiegelt die Tatsache, dass im Allgemeinen jeder Zweipol die Zweigspannungen und -ströme eines Netzwerks beeinflusst.
Durch eine systematische Vorgehensweise – nämlich der Knoten- und Maschenanalyse – lassen sich lineare Gleichungssysteme aufstellen, die eine gezielte Bestimmung von unbekannten Zweigspannungen beziehungsweise -strömen in einem Netzwerk ermöglichen. Im Rahmen einer Maschenanalyse könnten zum Beispiel die folgenden drei Gleichungen ermittelt worden sein:
