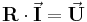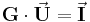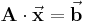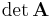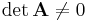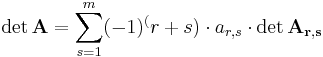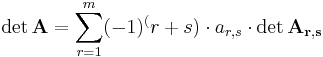Lineare Gleichungssysteme: Unterschied zwischen den Versionen
(→Matrizenrechnung) |
(→Matrizenrechnung) |
||
| Zeile 27: | Zeile 27: | ||
[[Multiplikation von Matrizen]] | [[Multiplikation von Matrizen]] | ||
| + | [[Inverse einer Matrix & Einheitsmatrix]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Determinante einer Matrix === | === Determinante einer Matrix === | ||
Version vom 4. Juli 2012, 16:49 Uhr
Eine Zusammenschaltung von verschiedenen aktiven oder passiven, linearen Zweipolen heißt Lineares Netzwerk. Es lässt sich durch lineare Gleichungssysteme beschreiben.
Um solch ein lineares Gleichungssystem aufzustellen, kann man die Kirchhoffschen Gesetze, also Maschen-, und Knotengleichungen verwenden. Dementsprechend wird eine Maschenanalyse angewandt, wenn die Ströme eines Netzwerks in einigen oder allen Zweigen gesucht sind. Sind die Spannungen gesucht, verwendet man die Knotenanalyse. Die Gleichungssysteme erhalten dabei folgende Formen:
oder
oder in allgemeiner Form:
Matrizen werden hier, um sie von anderen, zum Beispiel skalaren Größen zu unterscheiden fett gedruckt. Dabei können Vektoren als Sonderfall von Matrizen aufgefasst werden, die nur eine Spalte besitzen. Ebenfalls sollte beachtet werden, dass hier die gesuchten Größen bei diesen Gleichungen auf der linken Seite stehen, also auf der selben Seite wie die Widerstands- oder Leitwertmatrix.
 Beispiel: Knotenanalyse
|
Komponenten des linearen Gleichungsystems
Inhaltsverzeichnis
Matrizenrechnung
Multiplikation von Matrizen Inverse einer Matrix & Einheitsmatrix
Determinante einer Matrix
Eine quadratische Matrix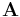 
wird auf eindeutige Weise einer bestimmten Zahl zugeordnet, diese Zahl heißt Determinante der Matrix, oder in mathematischer Schreibweise:
Die Determinante, ist dabei ein Maß für die Lösbarkeit eines linearen Gleichungssystems. Es gilt, wenn die Determinante ungleich null ist, also:
ist das System linear unabhängig und damit eindeutig lösbar. Umgekehrt gilt ebenso: Ist die Determinate gleich 0, gibt es unendlich viele verschiedene Lösungen und das System damit auch nicht linear unabhängig ist.
Berechnung der Determinante
In diesem Abschnitt sollen zwei Lösungsverfahren, zur Bestimmung der Determinante einer quadratischen Matrix besprochen werden.
a)
Das erste Lösungsverfahren, das Enwickeln der Matrix nach einer beliebigen Zeile oder Spalte ist ein Verfahren das allgemein gilt und immer verwendet werden kann.
Entwickelt man nach beliebiger Spalte (s-te Spalte), ergibt sich folgende Form:
oder man entwickelt nach einer beliebigen Zeile (r-te Zeile). Daraus folgt:
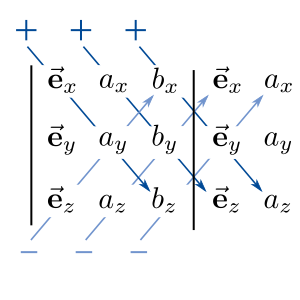
b) Das zweite Verfahren die Regel von Sarrus, gilt nur bei 3x3-Matrizen oder kleiner. Es ist allerdings viel weniger aufwendig.
Die Rechenvorschrift ist in der nebenstehenden Abbildung eingezeichnet. Dabei muss bei der 3x3 Matrix zunächst noch die ersten beiden Spalten angehängt werden, dieser Schritt fällt bei einer 2x2 Matrix weg . Dann muss man also nur nach dem "Maschendrahtzaun-Prinzip" erst alle diagonal von rechts oben nach links unten Verlaufenden Zahlenreihen multiplizieren und anschließend aufaddieren und anschließend diagonal in entgegengesetzer Richtung die Diagonalen multiplizieren und subtrahieren.
| Beispiel: Regel von Sarrus am Zahlenbeispiel
|
