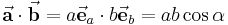Skalarprodukt: Unterschied zwischen den Versionen
Aus GET A
| Zeile 1: | Zeile 1: | ||
[[Datei:Vektorrechnung_Skalarprodukt.jpg|miniatur|Skalarprodukt]] | [[Datei:Vektorrechnung_Skalarprodukt.jpg|miniatur|Skalarprodukt]] | ||
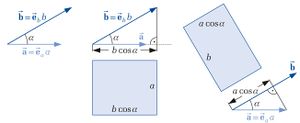
| − | Bei der Multiplikation zweier Vektoren handelt es sich entweder um das [[Vektorprodukt]] (auch Kreuzprodukt genannt) oder aber um das [[Skalarprodukt]]. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren <math>\vec{\textbf{a}}</math> und <math>\vec{\textbf{b}}</math>. | + | Bei der Multiplikation zweier Vektoren handelt es sich entweder um das [[Vektorprodukt]] (auch Kreuzprodukt genannt) oder aber um das [[Skalarprodukt]]. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren <math>\vec{\textbf{a}}</math> und <math>\vec{\textbf{b}}</math>. So ist das zugehörige Skalarprodukt wie folgt definiert: |
| + | :<math> | ||
| + | \vec{\textbf{a}} \cdot \vec{\textbf{b}} = a \vec{\textbf{e}}_{a} \cdot b\vec{\textbf{e}}_{b} = a b \cos \alpha | ||
| + | </math> | ||
| + | Dabei bezeichnet <math>\alpha</alpha> den Winkel, der von beiden Vektoren eingeschlossen wird und Werte zwischen <math>0</math> und <math>180^\circ</math> annehmen kann. | ||
<noinclude>====Literatur==== | <noinclude>====Literatur==== | ||
Version vom 3. Februar 2012, 17:53 Uhr
Bei der Multiplikation zweier Vektoren handelt es sich entweder um das Vektorprodukt (auch Kreuzprodukt genannt) oder aber um das Skalarprodukt. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren 
und 
. So ist das zugehörige Skalarprodukt wie folgt definiert:
Dabei bezeichnet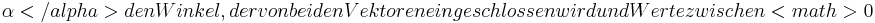 
und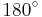 
annehmen kann.
