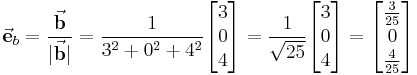Einheitsvektoren: Unterschied zwischen den Versionen
Aus GET A
| Zeile 18: | Zeile 18: | ||
:<math> | :<math> | ||
\vec{\textbf{e}}_{b} = \frac{\vec{\textbf{b}}}{|\vec{\textbf{b}}|} = | \vec{\textbf{e}}_{b} = \frac{\vec{\textbf{b}}}{|\vec{\textbf{b}}|} = | ||
| − | \frac{1}{3^2 + 0^2 + 4^2} \begin{bmatrix} 3 | + | \frac{1}{3^2 + 0^2 + 4^2} \begin{bmatrix} 3\\ 0\\ 4 \end{bmatrix} = |
| − | \frac{1}{\sqrt{25}} \begin{bmatrix} 3 | + | \frac{1}{\sqrt{25}} \begin{bmatrix} 3\\ 0\\ 4 \end{bmatrix} = |
| − | \begin{bmatrix} \frac{3}{25} | + | \begin{bmatrix} \frac{3}{25}\\ 0\\ \frac{4}{25} \end{bmatrix} |
</math> | </math> | ||
}} | }} | ||
Version vom 30. Januar 2012, 22:14 Uhr
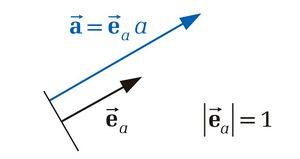
Unter einem Einheitsvektor versteht man allgemein einen Vektor mit dem Betrag beziehungsweise der Länge 1. Der Einheitsvektor 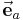 zu einem gegebenen Vektor
zu einem gegebenen Vektor  lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag dividiert:
lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag dividiert:
Der Vektor 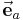 hat die Länge 1 (es gilt also
hat die Länge 1 (es gilt also 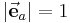 ) und zeigt in Richtung des Vektors
) und zeigt in Richtung des Vektors  . Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag und dem dazugehörigen Einheitsvektor angeben. Der Vektor
. Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag und dem dazugehörigen Einheitsvektor angeben. Der Vektor  kann somit auch wie folgt dargestellt werden:
kann somit auch wie folgt dargestellt werden:
Gegeben sei der Vektor |
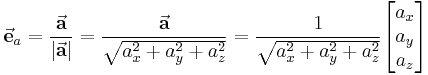
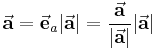
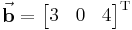 (das
(das 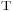 steht für
steht für