Difference between revisions of "Matrix inversion"
m (Nickchen moved page Matrixinversion to Matrix inversion) |
|
(No difference)
| |
Revision as of 15:09, 9 May 2014
The inverse of an n-by-n square matrix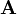 
is denoted as 
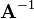and defined such that
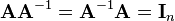
where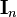 
is the n-by-n identity matrix.
Prerequesite for the inversion is, that 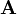is an n-by-n square matrix and that 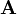is regular. Regular means that the row and column vectors are linearly independent and so the determinant is nonzero:
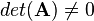
Otherwise the matrix is called singular.
Example:
![\begin{align}
\mathbf{A}_e\mathbf{A}_e^{-1} &=
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]\cdot
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]\\&=
\left[\begin{array}{cccc}
1+0+0+0 & 0+0+0+0 & -2+2+0+0 & 0+0+0+0\\
3+0+3-6 & 0+0-1+2 & -6+0-6+12 & 0+0+1-1\\
0+0+0+0 & 0+0+0+0 & 0+1+0+0 & 0+0+0+0\\
0+0+6-6 & 0+0-2+2 & 0+0-12+12 & 0+0+2-1
\end{array}\right]\\&=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{array}\right]=
\mathbf{I}_n
\end{align}](/wiki/robotics/images/math/e/2/e/e2ea26ac86532b1071f6ace97d659b98.png)
![\mathbf{A}_e =
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]
,\quad
\mathbf{A}_e^{-1} =
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]](/wiki/robotics/images/math/a/6/7/a67ba97d819f87ee26e95da04b416c0f.png)
Before determining the inverse of a matrix it is always useful to compute the determinant and check whether the matrix is regular or singular. If it is singular it is not possible to determine the inverse because there is no inverse. For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. To compute the determinant of larger matrices the following paragraph describes an example formula for a 4-by-4 matrix.
To determine the inverse of a matrix there are several alternatives. Two of the common procedures are the Gauß-Jordan-Algorithm and the Adjugate Formula that are explained afterwards.
