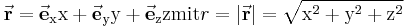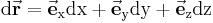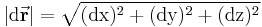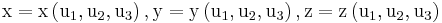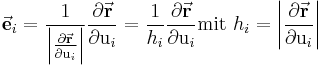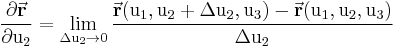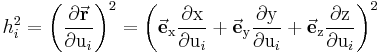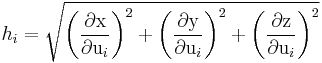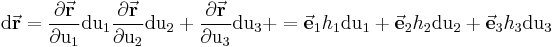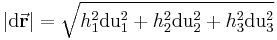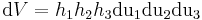Kartesische Koordinaten
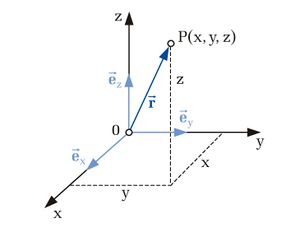
Den einfachsten Fall stellt das kartesische Koordinatensystem dar, bei dem die als x-, y- und z-Achse bezeichnet geradlinigen Koordinatenachsen zueinander orthogonal sind. Ihr gemeinsamer Schnittpunkt wird als Koordinatenursprung bzw. direkt als Ursprung bezeichnet. Die Richtung wachsender Koordinatenwerte wird für die Achsen so festgelegt, dass die Einheitsvektoren 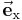 ,
, 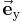 ,
, 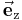 , die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
, die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
Eine Besonderheit beim kartesischen Koordinatensystem besteht darin, dass die Richtung der Einheitsvektoren aufgrund der geradlinigen Koordinaten x, y, z konstant, d. h. unabhängig von deren Position im Raum ist.
Als Koordinatenflächen erhält man die drei orthogonal zueinander angeordneten Ebenen x = const. (entspricht der y-z-Ebene), y = const. (entspricht der x-z-Ebene) und z = const. (entspricht der x-y-Ebene).
Der Raumpunkt P wird bezogen auf den Koordinatenursprung 0 durch den Ortsvektor 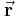 der Länge
der Länge 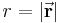 beschrieben:
beschrieben:
Formel (1)
Die differentielle Änderung des Ortsvektors 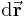 beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz in Richtung der gleichnamigen Koordinaten
beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz in Richtung der gleichnamigen Koordinaten
wird vektorielles Wegelement genannt. Seine Länge ist durch die Beziehung
gegeben.
Multimediale Lehrmaterialien
|
http://www.mathe-online.at/mathint/zeich/applet_b_kartes.htmlApplet: Kartesische Koordinaten im zweidimensionalem Raum http://www.mathe-online.at/mathint/zeich/applet_b_schief.html Applet: Schiefwinkliges Koordinatensystem im zweidimensionalem Raum http://www.kleemannschule.de/de/unterricht/mathematik/punkt3D.html Applet: Ein Punkt im dreidimensionalem Raum mit seinen Ortsvektoren |
Hilfreiche Links
|
http://cnx.org/content/m13600/latest/ Übersicht zu verschiedenen Koordinatensystemen |
Krummlinige orthogonale Koordinatensysteme
Bevor wir die Zylinder- und Kugelkoordinaten behandeln, sollen einige allgemein gültige Zusammenhänge für krummlinige orthogonale Koordinatensysteme 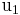 ,
, 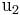 ,
, 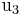 abgeleitet werden. Diese sind durch die im Allgemeinen bekannten Definitionsgleichungen:
abgeleitet werden. Diese sind durch die im Allgemeinen bekannten Definitionsgleichungen:
Formel (2)
mit den kartesischen Koordinaten verknüpft.
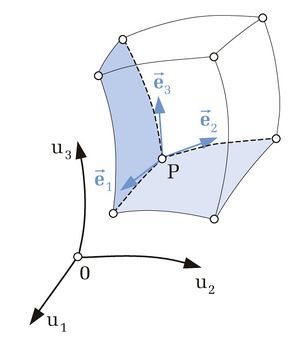
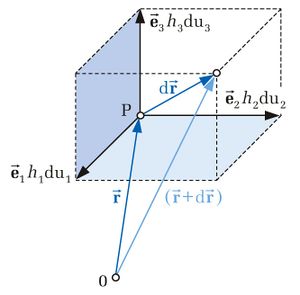
Das in Abbildung 3 dargestellte Volumen wird durch die sechs beliebig geformten Koordinatenflächen begrenzt, auf denen jeweils eine der Koordinaten 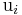 mit
mit 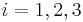 konstant ist. Die Einheitsvektoren
konstant ist. Die Einheitsvektoren 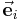 , die ??? und ??? erfüllen, zeigen in Richtung der Tangenten, die an die durch den Raumpunkt
, die ??? und ??? erfüllen, zeigen in Richtung der Tangenten, die an die durch den Raumpunkt 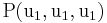 des Ortsvektors
des Ortsvektors 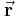 verlaufenden Koordinaten
verlaufenden Koordinaten 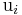 gelegt werden. Die Richtung dieser Tangenten und damit auch die Richtung der Einheitsvektoren ist durch die Änderung des Ortsvektors
gelegt werden. Die Richtung dieser Tangenten und damit auch die Richtung der Einheitsvektoren ist durch die Änderung des Ortsvektors 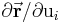 nach der jeweiligen Koordinate
nach der jeweiligen Koordinate 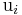 gegeben (*). Normiert man diesen Ausdruck auf seinen Betrag
gegeben (*). Normiert man diesen Ausdruck auf seinen Betrag 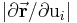 , dann lässt sich folgende Darstellung für die Einheitsvektoren angeben:
, dann lässt sich folgende Darstellung für die Einheitsvektoren angeben:
Formel (3)
(*) Unter dem Ausdruck 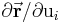 wird die partielle Ableitung, d. h. die Änderungsgeschwindigkeit des Ortsvektors
wird die partielle Ableitung, d. h. die Änderungsgeschwindigkeit des Ortsvektors 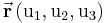 nach
nach 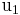 bzw.
bzw. 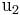 bzw.
bzw. 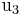 verstanden, wobei die jeweils anderen beiden Koordinaten konstant gehalten werden. Betrachten wir als Beispiel den Fall
verstanden, wobei die jeweils anderen beiden Koordinaten konstant gehalten werden. Betrachten wir als Beispiel den Fall 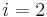 , dann gilt:
, dann gilt:
Entsprechend Formel (3) hängt also die Richtung der Einheitsvektoren im allgemeinen Fall von den Koordinaten 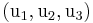 , d. h. von der Lage des Raumpunktes P ab. Die als metrische Faktoren bezeichneten Werte
, d. h. von der Lage des Raumpunktes P ab. Die als metrische Faktoren bezeichneten Werte 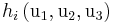 findet man mithilfe der Definitionsgleichungen Formel (2) aus:
findet man mithilfe der Definitionsgleichungen Formel (2) aus:
beziehungsweise:
Formel (4)
Bildet man nun das totale Differential 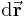 des Ortsvektors
des Ortsvektors 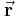 , das einer Änderung der Koordinatenwerte
, das einer Änderung der Koordinatenwerte 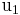 ,
, 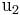 ,
, 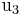 um
um 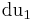 ,
, 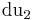 ,
, 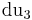 entspricht, dann erhält man unter Einbeziehung der Formel (3) das folgende Ergebnis:
entspricht, dann erhält man unter Einbeziehung der Formel (3) das folgende Ergebnis:
Formel (5)
Für den Betrag des vektoriellen Wegelementes gilt mit Gl. X (Verweis auf Vektoren) die Beziehung:
Formel (6) Das elementare Volumenelement erhält man durch Multiplikation der Seitenlängen gemäß Abbildung 4:
Formel (7)