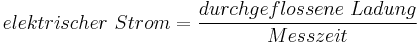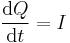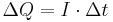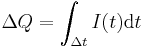Differentialquotient

In der nebenstehenden Abbildung ist eine Ladungsänderung im Leiterquerschnitt zu sehen. Dort wird eine gewisse Ladung pro Zeitintervall betrachtet. Diese Ladung pro Zeit ist nichts anderes als ein Strom.

$elektrischer~Strom=\frac{durchgeflossene~Ladung}{Messzeit}$

oder als Formel:

$I= \frac{\Delta Q}{\Delta t}$

Der Strom kann sowohl von den Ladungsträgern 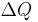$\Delta Q$ als auch durch das Zeitintervall 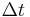$\Delta t$ bestimmt werden. Das Gleicher Strom dabei nicht unbedingt gleiche Geschwindigkeit der Ladungsträger bedeutet wird dabei im folgenden deutlich:

Wenn viele Ladungsträger langsam durch eine Testfläche fließen, kann das die gleiche Stromstärke bedeuten, wie wenn relativ wenig Ladungsträger sich schnell durch die Testfläche bewegen. Betrachtet man einen relativ großen Zeitintervall ist nicht zu erkennen, ob die Ladungsträger möglicherweise nicht gleichmäßig verteilt sind oder sich unterschiedlich schnell bewegen. Deswegen wird durch den Quotienten 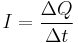$I= \frac{\Delta Q}{\Delta t}$ immer nur die mittlere Stromstärke im Intervall 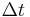$\Delta t$ bestimmt. Möchte man aber den Momentanwert an einer Stelle berechnen I(t), so muss man das Zeitintervall 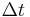$\Delta t$ immer kleiner machen. Dabei wird die Ladungsmenge 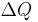$\Delta Q$, die in diesem Zeitbereich fließt auch immer kleiner.

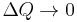Für $\Delta t\rightarrow 0$, oder auch $\Delta Q\rightarrow 0$, was auf das selbe hinausläuft, nähert sich der Quotient einem Grenzwert, der dem Momentanwert des Stromes zum Zeitpunkt t entspricht.

Dieser Grenzwert wird als

$\frac{\mathrm{d}Q}{\mathrm{d}t}=I$

bezeichnet.

Beispiel: Konstanter Strom im Vergleich zum variablen Strom Bei einem konstanten Strom I lässt sich die Ladung, die in der Zeit $\Delta t$ durch beispielsweise ein Kabel geflossen ist, durch die Fläche unter der Geraden I im Bereich $\Delta t$ darstellen (siehe Abbildung). Ganz analog folgt die Berechnung dazu: $\Delta Q= I\cdot\Delta t$ Ist der Strom zeitlich variabel, muss über I(t) integriert werden um die Fläche und so die durchflossene Ladnung zu bestimmen. $\Delta Q=\int_{\Delta t} I(t) \mathrm{d}t$ Betrachtet man den Quotienten $I= \frac{\Delta Q}{\Delta t}$:

Multimediale Lehrmaterialien

http://oberprima.com/mathematik/differentialquotient-ausfuehrliche-grafische-erklaerung-3569/ Video zur anschaulichen Erläuterung des Differenzenquotienten

Literatur

• Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
• www.leifiphysik.de
• wikiversity Kurs: Infinitesimal-Rechnung' Stand: 10. Oktober 2010
• Jänich, Mathematik 1: Für Physiker