Hauptseite/Farbige Gleichungen

Dieser Artikel befindet sich noch im Aufbau.

$\definecolor{gelb}{RGB}{255,165,0}$ $\definecolor{blau}{RGB}{0,165,255}$ $\definecolor{rot}{RGB}{255,0,0}$ $\definecolor{lila}{RGB}{165,0,255}$ $\definecolor{hellgruen}{RGB}{60,200,0}$ $\definecolor{pink}{RGB}{255,20,147}$ $\definecolor{orange}{RGB}{255,75,0}$ $\definecolor{dunkelgruen}{RGB}{90,125,0}$

In diesem Artikel werden zentrale Zusammenhänge der Lehrveranstaltung gemäß der Idee der Colorized Math Equations erläutert.

Satz von Gauß

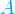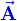Die Integration der elektrischen Flussdichte $\definecolor{gelb}{RGB}{255,165,0}\color{gelb}{\vec{\textbf{D}}}$ über eine beliebige geschlossene Hüllfläche $\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ ($\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\mathrm{d}}$$\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\vec{\textbf{A}}}$ ist ein differentielles gerichtetes Flächenelement von 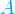$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$) liefert die in der Hüllfläche 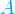$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ eingeschlossene Ladungsmenge $\definecolor{lila}{RGB}{165,0,255}\color{lila}{Q_\text{eing}}$. Diese Ladungsmenge entspricht der Integration der Raumladungsdichte 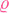$\definecolor{pink}{RGB}{255,75,145}\color{pink}{\varrho}$ über das Volumen 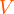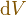$\definecolor{orange}{RGB}{255,80,0}\color{orange}{V}$ ($\definecolor{orange}{RGB}{130,85,0}\color{orange}{\mathrm{d}V}$ ist ein differentlielles Volumenelement des Volumens 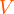$\definecolor{orange}{RGB}{255,80,0}\color{orange}{V}$), das von der geschlossenen Hüllfläche 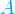$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ begrenzt wird. Die Hüllfläche 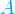$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ ist also der Rand des Volumens $\definecolor{orange}{RGB}{255,80,0}\color{orange}{V}$.

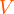Durchflutungsgesetz

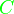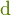
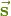Die Integration der magnetischen Feldstärke $\definecolor{dunkellila}{RGB}{100,60,100}\color{dunkellila}{\vec{\textbf{H}}}$ über eine geschlossene Kontur $\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ ($\definecolor{dgruen}{RGB}{90,125,0}\color{dgruen}{\mathrm{d}}$$\definecolor{dgruen}{RGB}{90,125,0}\color{dgruen}{\vec{\textbf{s}}}$ ist ein differentielles gerichtetes Wegelement der Kontur 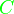$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$) liefert den in der Kontur 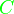$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ eingeschlossenen Strom 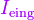$\definecolor{lila}{RGB}{165,0,255}\color{lila}{I_\text{eing}}$. Der eingeschlossenen Strom 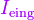$\definecolor{lila}{RGB}{165,0,255}\color{lila}{I_\text{eing}}$ entspricht der Integration der Stromdichte 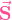$\definecolor{pink}{RGB}{255,75,145}\color{pink}{\vec{\textbf{S}}}$ über die Fläche 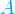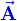$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ ($\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\mathrm{d}}$$\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\vec{\textbf{A}}}$ ist ein differentielles gerichtetes Flächenelement von 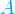$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$), die von der geschlossenen Kontur 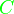$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ begrenzt wird. Die geschlossene Kontur 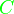$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ ist also der Rand der Fläche $\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$.

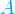Induktionsgesetz

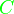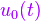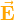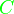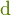
Die in eine Leiterschleife entlang der geschlossenen Kontur $\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ induzierte Spannung $\definecolor{lila}{RGB}{165,0,255}\color{lila}{u_0(t)}$ entspricht der Integration der elektrischen Feldstärke $\definecolor{gelb}{RGB}{255,165,0}\color{gelb}{\vec{\textbf{E}}}$ entlang dieser geschlossenen Kontur 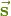$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ ($\definecolor{dgruen}{RGB}{90,125,0}\color{dgruen}{\mathrm{d}}$$\definecolor{dgruen}{RGB}{90,125,0}\color{dgruen}{\vec{\textbf{s}}}$ ist ein differentielles gerichtetes Wegelement der Kontur 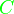$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$). Gleichzeitig entspricht die induzierte Spannung 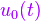$\definecolor{lila}{RGB}{165,0,255}\color{lila}{u_0(t)}$ der negativen zeitlichen Ableitung des magnetischen Flusses 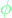$\definecolor{tuerkis}{RGB}{100,255,140}\color{tuerkis}{\phi}$. Der magnetische Fluss 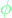$\definecolor{tuerkis}{RGB}{100,255,140}\color{tuerkis}{\phi}$ lässt sich wiederum durch die Integration der magnetischen Flussdichte 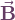$\definecolor{dunkellila}{RGB}{100,60,100}\color{dunkellila}{\vec{\textbf{B}}}$ über die Fläche 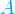$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$ bestimmen (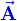$\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\mathrm{d}}$$\definecolor{dblau}{RGB}{0,0,255}\color{dblau}{\vec{\textbf{A}}}$ ist ein differentielles gerichtetes Flächenelement von 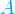$\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$), die von der geschlossenen Kontur 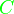$\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ begrenzt wird. 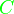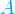Die geschlossene Kontur $\definecolor{gruen}{RGB}{0,255,0}\color{gruen}{C}$ ist also der Rand der Fläche $\definecolor{blau}{RGB}{0,165,255}\color{blau}{A}$.