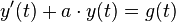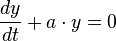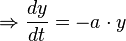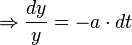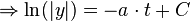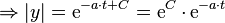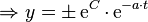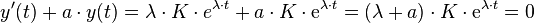Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 1. Ordnung

Gegeben sei eine inhomogene Differenzialgleichung 1. Ordnung mit konstanten Koeffizienten. Diese DGL lässt sich allgemein schreiben als

$y'(t)+a \cdot y(t)=g(t)$

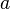wobei $a$ eine Konstante ist. Die Lösung erfolgt in vier Schritten:

1. Lösung der dazugehörigen homogenen DGL
2. Finden einer partikulären Lösung der inhomogenen DGL
3. Addieren der beiden Lösungen liefert die allgemeine Lösung der inhomogenen DGL
4. Berücksichtigung von Anfangsbedingungen

Lösung der homogenen linearen Differenzialgleichung

Die zur inhomogenen DGL dazugehörige homogene DGL lautet:

$y'(t)+a \cdot y(t)=0$

Zur Herleitung der Lösung wird nun das Verfahren „Trennung der Variablen“ angewandt. Dabei wird die Gleichung so umgestellt, dass die eine Seite der Gleichung nur noch von 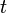$t$, und die andere Seite der Gleichung nur noch von 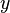$y$ abhängt. Nun werden beide Seiten der Gleichung integriert und daraus ergibt sich dann die Lösung für $y$.

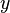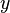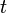Für die bessere Übersichtlichkeit wird die Abhängigkeit der Funktion $y$ von $t$ im Folgenden nicht explizit angegeben (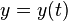$y=y(t)$) und für deren Ableitung 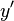$y'$ wird die Schreibweise 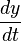$\frac{dy}{dt}$ genutzt:

$\frac{dy}{dt} +a \cdot y = 0$

$\Rightarrow \frac{dy}{dt} = -a \cdot y$

$\Rightarrow \frac{dy}{y}=-a \cdot dt$

Nun folgt die Integration. Dabei werden die Integrationskonstanten beider Integrale zu einer gemeinsamen Integrationskonstante 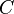$C$ zusammengefasst.

$\int \frac{1}{y} dy = - \int a \cdot dt$

$\Rightarrow \ln(|y|) = -a \cdot t + C$

$\Rightarrow |y| = \operatorname{e}^{-a \cdot t + C} =\operatorname{e}^C \cdot \operatorname{e}^{-a \cdot t}$

$\Rightarrow y = \pm \operatorname{e}^C \cdot \operatorname{e}^{-a \cdot t}$

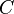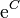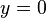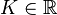Da die Integrationskonstante $C$ alle reellen Zahlen durchläuft, kann $\operatorname{e}^C$ beliebige positive Werte annehmen. Der Ausdruck $\pm \operatorname{e}^C$ durchläuft damit alle von 0 verschiedene, reelle Werte. Auch $y=0$ ist eine Lösung der homogenen DGL, weshalb $\pm \operatorname{e}^C$ durch die Konstante $K \in \R$ ersetzt werden kann. Die allgemeine Lösung der homogenen linearen Differenzialgleichung 1. Ordnung lautet damit:

$y_{h}(t) = K \cdot \operatorname{e}^{-a \cdot t} \text{ mit } K \in \R$

Der Index 'h' deutet an, dass es sich um die allgemeine Lösung der homogenen DGL handelt.

Hinweis: Das Verfahren kann auch bei nicht konstanten Koeffizienten angewandt werden, um eine homogene lineare DGL erster Ordnung zu lösen. Einzige Bedingung an den Koeffizienten ist, dass dieser eine integrierbare Funktion sein muss.

Exponentialansatz

Mit dem Verfahren „Trennung der Variablen“ kommt man ohne Vorkenntnisse auf den Exponentialansatz zur Lösung der DGL. Bei der Lösung von Differentialgleichungen besteht jedoch auch die Möglichkeit, eine Lösung zu vermuten. Wenn eine Funktion die Differentialgleichung und auch die Randbedingungen einer Aufgabe erfüllt, so ist diese Funktion eine gültige Lösung der DGL. Statt das Verfahren „Trennung der Variablen“ anzuwenden, kann bei einer linearen DGL 1. Ordnung mit konstanten Koeffizienten auch der Exponentialansatz 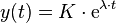$y(t) = K \cdot \operatorname{e}^{\lambda \cdot t}$ direkt in die homogene DGL eingesetzt werden. Mit der Ableitung $y'(t)=\lambda \cdot K \cdot e^{\lambda \cdot t}$ ergibt sich dann:

$y'(t) + a \cdot y(t) = \lambda \cdot K \cdot e^{\lambda \cdot t} + a \cdot K \cdot \operatorname{e}^{\lambda \cdot t} = (\lambda + a) \cdot K \cdot \operatorname{e}^{\lambda \cdot t} = 0$