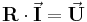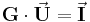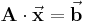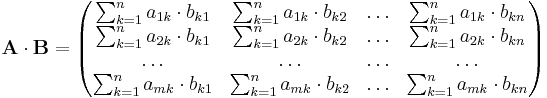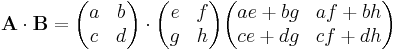Lineare Gleichungssysteme
Eine Zusammenschaltung von verschiedenen aktiven oder passiven, linearen Zweipolen heißt Lineares Netzwerk. Es lässt sich durch lineare Gleichungssysteme beschreiben.
Um solch ein lineares Gleichungssystem aufzustellen, kann man die Kirchhoffschen Gesetze, also Maschen-, und Knotengleichungen verwenden. Dementsprechend wird eine Maschenanalyse angewandt, wenn die Ströme eines Netzwerks in einigen oder allen Zweigen gesucht sind. Sind die Spannungen gesucht, verwendet man die Knotenanalyse. Die Gleichungssysteme erhalten dabei folgende Formen:
oder
oder in allgemeiner Form:
Matrizen werden hier, um sie von anderen, zum Beispiel skalaren Größen zu unterscheiden fett gedruckt. Dabei können Vektoren als Sonderfall von Matrizen aufgefasst werden, die nur eine Spalte besitzen. Ebenfalls sollte beachtet werden, dass hier die gesuchten Größen bei diesen Gleichungen auf der linken Seite stehen, also auf der selben Seite wie die Widerstands- oder Leitwertmatrix.
Inhaltsverzeichnis
Einzelteile des Linearen Gleichungssystems
Koeffizientenmatrix
Die Koeffizientenmatrix, oben auch Widerstands-, oder Leitwertmatrix genannt, enthält alle in den Maschen vorkommenden Widerstände oder Leitwerte. Sie ist aus m Zeilen und n Spalten aufgebaut ((m x n )-Matrix). Dabei hat sie immer folgende Form:
Die Elemente der Matrix 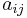 sollen hier nur rein reelwertig angenommen werden. Man beachte die Reihenfolge, sodass i der Zeilenindex und j der Spaltenindex ist.
sollen hier nur rein reelwertig angenommen werden. Man beachte die Reihenfolge, sodass i der Zeilenindex und j der Spaltenindex ist.
Die Spaltenvektoren
Die Spaltenvektoren  und
und 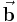 entsprechen in den hier betrachteten Fällen immer Strömen und Spannungen. Sie haben folgende Form:
entsprechen in den hier betrachteten Fällen immer Strömen und Spannungen. Sie haben folgende Form:
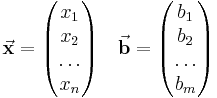
Dabei ist zu beachten das der  -Vektor immer die gesuchten Größen enthält.
-Vektor immer die gesuchten Größen enthält.
Matrizenrechnung
Multiplikation zweier Matrizen
Möchte man zwei Matrizen multiplizieren, gibt es ein bestimmtes Rechenschema, dass eingehalten werden muss. Dabei ist es wichtig, dass die Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix übereinstimmt. Dies impliziert auch, dass die Matrizenmultiplikation nicht kommuntativ ist, also die Matrizen in einer Rechnung auf keinen Fall getauscht werden dürfen.
Um nun das erste Element der neuen Matrix zu berechnen, muss man das erste Element der ersten Zeile der ersten Matrix mit dem ersten Element der ersten Spalte der zweiten Matrix multiplizieren und anschließend das zweite Element der ersten Zeile der ersten Matrix mit dem zweiten Element der ersten Spalte der zweiten Matrix multipliziert und die Ergebnisse der Multiplikationen aufaddiert werden. Dies führt man solange durch, bis das letzte Element der ersten Zeile der ersten Matrix und das letzte Element der ersten Spalte der zweiten Matrix erreicht ist. Daraus folgt auch, die Gleichheit der Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix, die vorher schon gefordert wurde.
Einfacher wird es wenn man sich zwei kleine Matrizen, als beispiel 2 2x2-Matrizen anschaut. Dort lautet das Rechenschema: