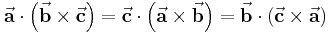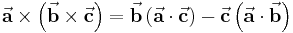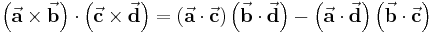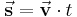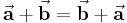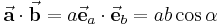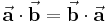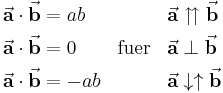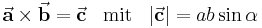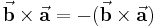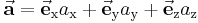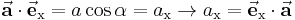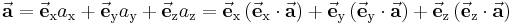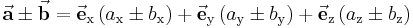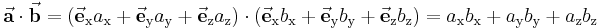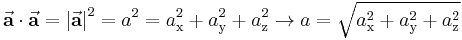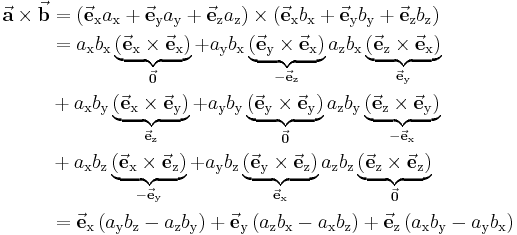Vektorrechnung
Inhaltsverzeichnis
Einführung
In der Physik werden viele Größen durch Zahlenwert und Einheit vollständig beschrieben wie z. B. das Gewicht eines Körpers oder die Temperatur. Man spricht in diesem Fall von skalaren Größen. Daneben existieren vektorielle Größen, zu deren Beschreibung neben Zahlenwert und Einheit auch noch die Richtung benötigt wird. Betrachten wir z. B. die Bewegung eines Flugkörpers, dann besitzt dieser zu jedem Zeitpunkt nicht nur eine momentane Geschwindigkeit v(t), sondern auch eine Bewegungsrichtung. Während die gerichteten Größen durch Vektoren dargestellt werden, erfolgt die Beschreibung der physikalischen Zusammenhänge durch vektorielle Größengleichungen. Die gerichtete Strecke  kann z. B. als das Produkt aus gerichteter Geschwindigkeit
kann z. B. als das Produkt aus gerichteter Geschwindigkeit 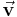 und Zeit t berechnet werden:
und Zeit t berechnet werden:
Formel (1)
In einer vektoriellen Gleichung erfüllen Zahlenwerte, Einheiten und Richtung unabhängig voneinander die Gleichheitsbeziehung.
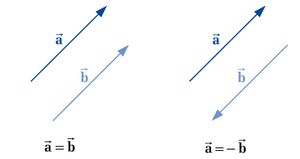
Zeichnerisch werden Vektoren durch Pfeile dargestellt, deren Richtung die Richtung des Vektors angibt und deren Länge den Betrag des Vektors beschreibt. Zwei Vektoren werden als gleich bezeichnet, wenn sowohl ihr Betrag, ihre Orientierung im Raum als auch ihr Durchlaufsinn gleich sind. In der Physik unterscheidet man zwischen freien Vektoren und gebundenen Vektoren. Bei freien Vektoren spielt die Position ihres Anfangspunktes keine Rolle, d. h. sie können frei im Raum verschoben werden. Zwei gleiche Vektoren können so durch paralleles Verschieben zur Deckung gebracht werden. Als Beispiel für die gebundenen Vektoren können die Feldvektoren angesehen werden, die z. B. Betrag und Richtung einer ortsabhängigen Feldstärke beschreiben und damit einer bestimmten Stelle im Raum zugeordnet sind. Bei gebundenen Vektoren können Betrag und Richtung in jedem Punkt des Raumes unterschiedlich sein.
Unter einem Vektor 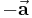 versteht man einen Vektor mit dem gleichen Betrag wie
versteht man einen Vektor mit dem gleichen Betrag wie 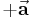 , aber mit entgegengesetzter Richtung.
, aber mit entgegengesetzter Richtung.
In vielen Fällen werden unterschiedliche Vektoren benötigt, die aber den gleichen Angriffspunkt haben, z. B. kann man sich mehrere Vektoren vorstellen, die ausgehend von dem Ursprung eines Koordinatensystems zu verschiedenen Punkten im dreidimensionalen Raum zeigen. Diese Vektoren werden als Ortsvektoren bezeichnet.
Einheitsvektoren
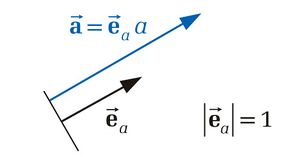
Ein Vektor vom Betrag 1 wird Einheitsvektor genannt. Jeder Vektor kann als Produkt aus einem Betrag (seiner Länge) und einem in Richtung des Vektors zeigenden Einheitsvektor dargestellt werden.
Den in Richtung eines Vektors  zeigenden Einheitsvektor
zeigenden Einheitsvektor 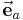 kann man nach Formel (1) berechnen, indem man den Vektor durch seinen Betrag a dividiert.
kann man nach Formel (1) berechnen, indem man den Vektor durch seinen Betrag a dividiert.
Einfache Rechenoperationen mit Vektoren
Addition und Subtraktion von Vektoren
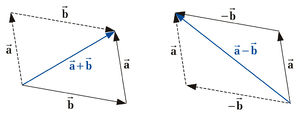
Zwei Vektoren werden addiert, indem man den zweiten Vektor parallel verschiebt, dass sein Anfangspunkt mit dem Endpunkt des ersten Vektors zusammenfällt. Der resultierende Vektor (Summenvektor) ist ein neuer Vektor, dessen Anfangspunkt mit dem Anfangspunkt des ersten Vektors und dessen Endpunkt mit dem Endpunkt des zweiten Vektors zusammenfällt.
Aus der Abbildung 3 ist unmittelbar zu erkennen, dass für die Vektoraddition das kommutative Gesetz gilt
Zur Berechnung des Differenzvektors  bildet man zunächst den Vektor
bildet man zunächst den Vektor 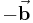 , indem man bei dem Vektor
, indem man bei dem Vektor 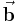 die Richtung umkehrt. Dieser neue Vektor wird dann zum Vektor
die Richtung umkehrt. Dieser neue Vektor wird dann zum Vektor  gemäß der Vorschrift
gemäß der Vorschrift
addiert Abbildung 3.
Multiplikation von Vektor und Skalar
Bezeichnet man mit p eine positive reelle Zahl, dann versteht man unter dem Produkt  einen Vektor mit der gleichen Richtung wie
einen Vektor mit der gleichen Richtung wie  , dessen Länge
, dessen Länge 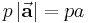 sich aber um den Faktor p geändert hat. Handelt es sich bei p um eine negative Zahl, dann versteht man unter dem Produkt p a einen neuen Vektor der Länge
sich aber um den Faktor p geändert hat. Handelt es sich bei p um eine negative Zahl, dann versteht man unter dem Produkt p a einen neuen Vektor der Länge  , jetzt aber mit entgegengesetzter Richtung zu dem ursprünglichen Vektor
, jetzt aber mit entgegengesetzter Richtung zu dem ursprünglichen Vektor  . Für den Sonderfall p = 0 erhält man aus dem Produkt
. Für den Sonderfall p = 0 erhält man aus dem Produkt 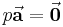 den Nullvektor
den Nullvektor 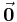 mit der Länge 0, dessen Richtung unbestimmt ist.
mit der Länge 0, dessen Richtung unbestimmt ist.
Skalarprodukt
Das Skalarprodukt 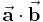 zweier Vektoren
zweier Vektoren  und
und 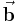 ist definiert als
ist definiert als
Formel (2)
wobei 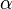 den von den beiden Vektoren eingeschlossenen Winkel bezeichnet, sofern beide Vektoren an dem gleichen Anfangspunkt beginnen. Das Ergebnis dieser Berechnung ist ein Skalar. Der Winkel
den von den beiden Vektoren eingeschlossenen Winkel bezeichnet, sofern beide Vektoren an dem gleichen Anfangspunkt beginnen. Das Ergebnis dieser Berechnung ist ein Skalar. Der Winkel 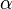 liegt zwischen 0 und 180°, d. h. der Kosinus dieses Winkels ist eindeutig.
liegt zwischen 0 und 180°, d. h. der Kosinus dieses Winkels ist eindeutig.
Die Länge 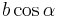 kann interpretiert werden als die Länge der Strecke, die man bei einer Projektion des Vektors
kann interpretiert werden als die Länge der Strecke, die man bei einer Projektion des Vektors 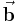 auf die Richtung des Vektors
auf die Richtung des Vektors  erhält.
erhält.
Das Skalarprodukt entspricht also dem Flächeninhalt des Rechtecks mit den Seitenlängen 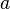 und
und 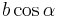 . Mit der gleichen Berechtigung kann auch der Vektor
. Mit der gleichen Berechtigung kann auch der Vektor  auf die Richtung des Vektors
auf die Richtung des Vektors 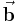 projiziert werden. Das Produkt aus der Länge dieser Projektion
projiziert werden. Das Produkt aus der Länge dieser Projektion 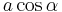 mit der Länge
mit der Länge  ergibt wiederum ein Rechteck mit geändertem Seitenverhältnis, jedoch gleichem Flächeninhalt.
ergibt wiederum ein Rechteck mit geändertem Seitenverhältnis, jedoch gleichem Flächeninhalt.
Aus der Beziehung Formel (2) bzw. aus der Abbildung 4 ist unmittelbar zu erkennen, dass das Skalarprodukt kommutativ ist
Für parallele bzw. senkrecht aufeinander stehende Vektoren  und
und 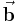 erhält man die Sonderfälle
erhält man die Sonderfälle
Vektorprodukt
Zur Beschreibung einiger physikalischer Zusammenhänge wie z. B. bei der Berechnung der Kraft auf einen stromdurchflossenen Leiter oder bei der Berechnung des Drehmomentes wird noch eine andere Verknüpfung von Vektoren benötigt, die als Vektorprodukt oder auch Kreuzprodukt bezeichnet wird.
Das vektorielle Produkt 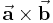 bei beiden Vektoren
bei beiden Vektoren  und
und 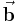 ist ein Vektor
ist ein Vektor 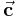 , der senkrecht auf der von den beiden Vektoren
, der senkrecht auf der von den beiden Vektoren  und
und 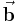 aufgespannten Ebene steht und dessen Richtung so festgelegt ist, dass die drei Vektoren
aufgespannten Ebene steht und dessen Richtung so festgelegt ist, dass die drei Vektoren  ,
, 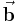 ,
, 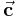 ein Rechtssystem bilden. Beim Drehen des Vektors
ein Rechtssystem bilden. Beim Drehen des Vektors  in Richtung des Vektors
in Richtung des Vektors 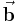 erfährt er eine Rechtsschraube eine Vorwärtsbewegung in Richtung des Vektors
erfährt er eine Rechtsschraube eine Vorwärtsbewegung in Richtung des Vektors 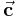 . Man kann sich diesen Zusammenhang auch auf einfache Weise mit den Fingern der rechten Hand veranschlaulichen. Zeigt der Daumen in Richtung des Vektors
. Man kann sich diesen Zusammenhang auch auf einfache Weise mit den Fingern der rechten Hand veranschlaulichen. Zeigt der Daumen in Richtung des Vektors  und der Zeigefinger in Richtung des Vektors
und der Zeigefinger in Richtung des Vektors 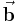 , dann zeigt der senkrecht auf der von den beiden Fingern gebildeten Ebene stehende Mittelfinger in Richtung des Vektors
, dann zeigt der senkrecht auf der von den beiden Fingern gebildeten Ebene stehende Mittelfinger in Richtung des Vektors 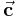 .
.
Als Betrag des Vektors 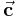 definiert man das Produkt
definiert man das Produkt 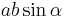 , das gemäß Abb. 5 dem Flächeninhalt des von beiden Vektoren
, das gemäß Abb. 5 dem Flächeninhalt des von beiden Vektoren  und
und 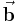 aufgespannten Parallelogramms entspricht
aufgespannten Parallelogramms entspricht
Der zwischen den Vektoren  und
und 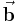 eingeschlossenen Winkel
eingeschlossenen Winkel 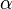 liegt in dem Wertebereich
liegt in dem Wertebereich 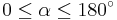 .
.
Wird der Vektor 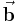 in Richtung des Vektors
in Richtung des Vektors  gedreht, dann zeigt die so entstehende Rechtsschraube in die entgegengesetzte Richtung, so dass allgemein
gedreht, dann zeigt die so entstehende Rechtsschraube in die entgegengesetzte Richtung, so dass allgemein
gilt. Das Vektorprodukt ist nicht kommutativ.
Für parallele bzw. senkrecht aufeinander stehende Vektoren  und
und 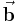 gelten die beiden Sonderfälle
gelten die beiden Sonderfälle
Zerlegung eines Vektors in seine Komponenten
In der Abbildung 3 wurde ein Vektor durch Summation aus zwei anderen Vektoren berechnet. In diesem Abschnitt soll der umgekehrte Vorgang, nämlich die Zerlegung eines gegebenen Vektors in zwei oder mehr einzelne Vektoren, man spricht in diesem Zusammenhang von den Komponenten eines Vektors, gezeigt werden. In der Praxis tritt häufig der Fall auf, dass die Richtungen der einzelnen Komponenten bereits vorgegeben sind, wobei üblicherweise die Einschränkung gilt, dass die Komponenten senkrecht aufeinander stehen. Die einfachste Aufgabe ist beispielsweise die Zerlegung eines beliebigen Vektors in drei Komponenten, von denen jede parallel zu einer Achse des kartesischen Koordinatensystems verläuft. Bezeichnet man mit 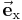 ,
, 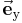 ,
, 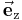 die Einheitsvektoren in Richtung der entsprechenden Achsen x, y, z, dann besteht die Aufgabe bei der Zerlegung eines Vektors
die Einheitsvektoren in Richtung der entsprechenden Achsen x, y, z, dann besteht die Aufgabe bei der Zerlegung eines Vektors  darin, die Längen der einzelnen Komponenten
darin, die Längen der einzelnen Komponenten 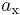 ,
, 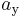 ,
, 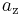 so zu bestimmen, dass deren Summation wieder den ursprünglichen Vektor ergibt:
so zu bestimmen, dass deren Summation wieder den ursprünglichen Vektor ergibt:
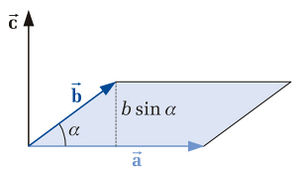
Als Beispiel betrachten wir die in Abbildung 6 dargestellte Zerlegung des in der xy-Ebene liegenden Vektors  in die beiden Komponenten in Richtung der im Bild ebenfalls dargestellten Einheitsvektoren
in die beiden Komponenten in Richtung der im Bild ebenfalls dargestellten Einheitsvektoren 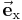 und
und 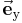 .
.
Die Länge 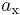 entspricht offenbar der Projektion des Vektors
entspricht offenbar der Projektion des Vektors  auf die parallel zu
auf die parallel zu 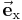 verlaufende Linie. Mit dem in der Abbildung eingetragenen Winkel
verlaufende Linie. Mit dem in der Abbildung eingetragenen Winkel 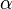 ist diese Länge durch den Ausdruck
ist diese Länge durch den Ausdruck 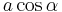 gegeben, den man mit der Definition des Skalarproduktes nach Formel (2) in der folgenden Form schreiben kann:
gegeben, den man mit der Definition des Skalarproduktes nach Formel (2) in der folgenden Form schreiben kann:
Die Komponente des Vektors  in Richtung des Einheitsvektors
in Richtung des Einheitsvektors 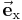 kann nach Abbildung 6 dargestellt werden als ein Produkt aus dem Einheitsvektor
kann nach Abbildung 6 dargestellt werden als ein Produkt aus dem Einheitsvektor 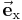 und der Länge
und der Länge 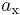 .
.
Führt man diese Betrachtung für alle drei Komponenten durch, dann kann die Vektorzerlegung in der folgenden Weise dargestellt werden:
Vektorbeziehung in Komponentendarstellung
In diesem Abschnitt sollen die bisher angegebenen Beziehungen nochmals mithilfe der Komponentenzerlegung (s. o.) formuliert werden:
Für den Sonderfall zweier gleicher Vektoren folgt:
Vorsicht: Aus der Gleichung 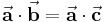 folgt im Allgemeinen nicht
folgt im Allgemeinen nicht 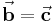 . Da es sich beim Skalarprodukt um eine Summation der Produkte aus den einzelnen Komponenten handelt, darf
. Da es sich beim Skalarprodukt um eine Summation der Produkte aus den einzelnen Komponenten handelt, darf  nicht gekürzt werden.
nicht gekürzt werden.
Formeln zur Vektorrechnung
Nachstehend sind einige Beziehungen angegeben, die (falls bisher nicht abgeleitet) mithilfe der Komponentenzerlegung leicht überprüft werden können.
Distributivität
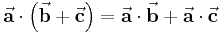
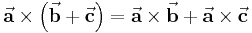
Assoziativität bezüglich der Multiplikation mit einer Zahl
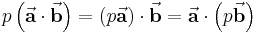

Mehrfache Produkte