Vektorrechnung: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
In der Physik werden viele Größen durch Zahlenwert und Einheit vollständig beschrieben wie z. B. das Gewicht eines Körpers oder die Temperatur. Man spricht in diesem Fall von '''skalaren''' Größen. Daneben existieren '''vektorielle''' Größen, zu deren Beschreibung neben Zahlenwert und Einheit auch noch die Richtung benötigt wird. Betrachten wir z. B. die Bewegung eines Flugkörpers, dann besitzt dieser zu jedem Zeitpunkt nicht nur eine momentane Geschwindigkeit v(t), sondern auch eine Bewegungsrichtung. Während die gerichteten Größen durch Vektoren dargestellt werden, erfolgt die Beschreibung der physikalischen Zusammenhänge durch vektorielle Größengleichungen. Die gerichtete Strecke <math>\vec{\textbf{s}}</math> kann z. B. als das Produkt aus gerichteter Geschwindigkeit <math>\vec{\textbf{v}}</math> und Zeit ''t'' berechnet werden: | In der Physik werden viele Größen durch Zahlenwert und Einheit vollständig beschrieben wie z. B. das Gewicht eines Körpers oder die Temperatur. Man spricht in diesem Fall von '''skalaren''' Größen. Daneben existieren '''vektorielle''' Größen, zu deren Beschreibung neben Zahlenwert und Einheit auch noch die Richtung benötigt wird. Betrachten wir z. B. die Bewegung eines Flugkörpers, dann besitzt dieser zu jedem Zeitpunkt nicht nur eine momentane Geschwindigkeit v(t), sondern auch eine Bewegungsrichtung. Während die gerichteten Größen durch Vektoren dargestellt werden, erfolgt die Beschreibung der physikalischen Zusammenhänge durch vektorielle Größengleichungen. Die gerichtete Strecke <math>\vec{\textbf{s}}</math> kann z. B. als das Produkt aus gerichteter Geschwindigkeit <math>\vec{\textbf{v}}</math> und Zeit ''t'' berechnet werden: | ||
<math> | <math> | ||
| − | |||
\vec{\textbf{s}} = \vec{\textbf{v}} \cdot t | \vec{\textbf{s}} = \vec{\textbf{v}} \cdot t | ||
| − | |||
</math> | </math> | ||
In einer vektoriellen Gleichung erfüllen Zahlenwerte, Einheiten und Richtung unabhängig voneinander die Gleichheitsbeziehung. | In einer vektoriellen Gleichung erfüllen Zahlenwerte, Einheiten und Richtung unabhängig voneinander die Gleichheitsbeziehung. | ||
Version vom 27. September 2011, 08:43 Uhr
Einführung
In der Physik werden viele Größen durch Zahlenwert und Einheit vollständig beschrieben wie z. B. das Gewicht eines Körpers oder die Temperatur. Man spricht in diesem Fall von skalaren Größen. Daneben existieren vektorielle Größen, zu deren Beschreibung neben Zahlenwert und Einheit auch noch die Richtung benötigt wird. Betrachten wir z. B. die Bewegung eines Flugkörpers, dann besitzt dieser zu jedem Zeitpunkt nicht nur eine momentane Geschwindigkeit v(t), sondern auch eine Bewegungsrichtung. Während die gerichteten Größen durch Vektoren dargestellt werden, erfolgt die Beschreibung der physikalischen Zusammenhänge durch vektorielle Größengleichungen. Die gerichtete Strecke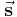 
kann z. B. als das Produkt aus gerichteter Geschwindigkeit 
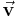und Zeit t berechnet werden:
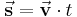In einer vektoriellen Gleichung erfüllen Zahlenwerte, Einheiten und Richtung unabhängig voneinander die Gleichheitsbeziehung.
Test Überschrift
Test: Addition:
Formel (1)
Hallo.
