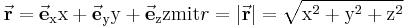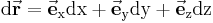|
|
| Zeile 73: |
Zeile 73: |
| | | | |
| | }} | | }} |
| − |
| |
| − | == Krummlinige orthogonale Koordinatensysteme ==
| |
| − | Bevor wir die Zylinder- und Kugelkoordinaten behandeln, sollen einige allgemein gültige Zusammenhänge für krummlinige orthogonale Koordinatensysteme <math>\mathrm{u}_1</math>, <math>\mathrm{u}_2</math>, <math>\mathrm{u}_3</math> abgeleitet werden. Diese sind durch die im Allgemeinen bekannten Definitionsgleichungen:
| |
| − | :<equation id="eqn:definition">
| |
| − | <math>
| |
| − | \mathrm{x} = \mathrm{x} \left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right),
| |
| − | \mathrm{y} = \mathrm{y} \left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right),
| |
| − | \mathrm{z} = \mathrm{z} \left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right)
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:definition" />
| |
| − |
| |
| − | mit den kartesischen Koordinaten verknüpft.
| |
| − | <figure id="fig:krummlinige_koordinaten">
| |
| − | [[Image:Koordinatensysteme_Krummlinige_Koordinaten.jpg|miniatur|<caption>Krummlinige Koordinaten</caption>]]
| |
| − | </figure>
| |
| − | Das in <xr id="fig:krummlinige_koordinaten"/> dargestellte Volumen wird durch die sechs beliebig geformten Koordinatenflächen begrenzt, auf denen jeweils eine der Koordinaten <math>\mathrm{u}_i</math> mit <math>i = 1, 2, 3</math> konstant ist. Die Einheitsvektoren <math>\vec{\textbf{e}}_i</math>, die <xr id="eqn:orthogonalitaet" /> und <xr id="eqn:wegelement" /> erfüllen, zeigen in Richtung der Tangenten, die an die durch den Raumpunkt <math>\mathrm{P}(\mathrm{u}_1, \mathrm{u}_1, \mathrm{u}_1)</math> des Ortsvektors <math>\vec{\textbf{r}}</math> verlaufenden Koordinaten <math>\mathrm{u}_i</math> gelegt werden. Die Richtung dieser Tangenten und damit auch die Richtung der Einheitsvektoren ist durch die Änderung des Ortsvektors <math>\partial \vec{\textbf{r}} / \partial \mathrm{u}_i</math> nach der jeweiligen Koordinate <math>\mathrm{u}_i</math> gegeben (*). Normiert man diesen Ausdruck auf seinen Betrag <math>\left| \partial \vec{\textbf{r}} / \partial \mathrm{u}_i \right|</math>, dann lässt sich folgende Darstellung für die Einheitsvektoren angeben:
| |
| − | :<equation id="eqn:einheitsvektoren">
| |
| − | <math>
| |
| − | \vec{\textbf{e}}_i = \frac{1}{\left|\frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i}\right|} \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} = \frac{1}{h_i} \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i}
| |
| − | \text{mit}\
| |
| − | h_i = \left| \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} \right|
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:einheitsvektoren"/>
| |
| − |
| |
| − | (*) Unter dem Ausdruck <math>\partial \vec{\textbf{r}} / \partial \mathrm{u}_i</math> wird die partielle Ableitung, d. h. die Änderungsgeschwindigkeit des Ortsvektors <math>\vec{\textbf{r}} \left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right)</math> nach <math>\mathrm{u}_1</math> bzw. <math>\mathrm{u}_2</math> bzw. <math>\mathrm{u}_3</math> verstanden, wobei die jeweils anderen beiden Koordinaten konstant gehalten werden. Betrachten wir als Beispiel den Fall <math>i=2</math>, dann gilt:
| |
| − | :<math>
| |
| − | \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_2} = \lim_{\Delta \mathrm{u}_2 \to 0}
| |
| − | \frac{\vec{\textbf{r}}(\mathrm{u}_1, \mathrm{u}_2 + \Delta \mathrm{u}_2, \mathrm{u}_3) - \vec{\textbf{r}}(\mathrm{u}_1 , \mathrm{u}_2, \mathrm{u}_3)}{\Delta \mathrm{u}_2}
| |
| − | </math>
| |
| − |
| |
| − | Entsprechend <xr id="eqn:einheitsvektoren" /> hängt also die Richtung der Einheitsvektoren im allgemeinen Fall von den Koordinaten <math>\left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right)</math>, d. h. von der Lage des Raumpunktes P ab. Die als metrische Faktoren bezeichneten Werte <math>h_i \left( \mathrm{u}_1, \mathrm{u}_2, \mathrm{u}_3 \right)</math> findet man mithilfe der Definitionsgleichungen <xr id="eqn:definition"/> aus:
| |
| − | :<math>
| |
| − | h_i^2 = \left( \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} \right)^2 =
| |
| − | \left(
| |
| − | \vec{\textbf{e}}_\mathrm{x} \frac{\partial \mathrm{x}}{\partial \mathrm{u}_i} +
| |
| − | \vec{\textbf{e}}_\mathrm{y} \frac{\partial \mathrm{y}}{\partial \mathrm{u}_i} +
| |
| − | \vec{\textbf{e}}_\mathrm{z} \frac{\partial \mathrm{z}}{\partial \mathrm{u}_i}
| |
| − | \right)^2
| |
| − | </math>
| |
| − | beziehungsweise:
| |
| − | :<equation id="eqn:metrisch">
| |
| − | <math>
| |
| − | h_i =
| |
| − | \sqrt{
| |
| − | \left( \frac{\partial \mathrm{x}}{\partial \mathrm{u}_i} \right)^2 +
| |
| − | \left( \frac{\partial \mathrm{y}}{\partial \mathrm{u}_i} \right)^2 +
| |
| − | \left( \frac{\partial \mathrm{z}}{\partial \mathrm{u}_i} \right)^2
| |
| − | }
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:metrisch"/>
| |
| − |
| |
| − | Bildet man nun das totale Differential <math>\mathrm{d}\vec{\textbf{r}}</math> des Ortsvektors <math>\vec{\textbf{r}}</math>, das einer Änderung der Koordinatenwerte <math>\mathrm{u}_1</math>, <math>\mathrm{u}_2</math>, <math>\mathrm{u}_3</math> um <math>\mathrm{d}\mathrm{u}_1</math>, <math>\mathrm{d}\mathrm{u}_2</math>, <math>\mathrm{d}\mathrm{u}_3</math> entspricht, dann erhält man unter Einbeziehung der <xr id="eqn:einheitsvektoren" /> das folgende Ergebnis:
| |
| − | :<equation id="eqn:total">
| |
| − | <math>
| |
| − | \mathrm{d}\vec{\textbf{r}} =
| |
| − | \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_1} \mathrm{d}\mathrm{u}_1
| |
| − | \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_2} \mathrm{d}\mathrm{u}_2 +
| |
| − | \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_3} \mathrm{d}\mathrm{u}_3 +
| |
| − | =
| |
| − | \vec{\textbf{e}}_1 h_1 \mathrm{d}\mathrm{u}_1 +
| |
| − | \vec{\textbf{e}}_2 h_2 \mathrm{d}\mathrm{u}_2 +
| |
| − | \vec{\textbf{e}}_3 h_3 \mathrm{d}\mathrm{u}_3
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:total"/>
| |
| − |
| |
| − | <figure id="fig:krummlinige_koordinaten2">
| |
| − | [[Image:Koordinatensysteme_Krummlinige_Koordinaten2.jpg|miniatur|<caption>Krummlinige Koordinaten</caption>]]
| |
| − | </figure>
| |
| − | Für den Betrag des vektoriellen Wegelementes gilt mit Gl. X (Verweis auf Vektoren) die Beziehung:
| |
| − | :<equation id="eqn:volumen">
| |
| − | <math>
| |
| − | \left| \mathrm{d}\vec{\textbf{r}} \right| =
| |
| − | \sqrt{h_1^2 \mathrm{d}\mathrm{u}_1^2 + h_2^2 \mathrm{d}\mathrm{u}_2^2 + h_3^2 \mathrm{d}\mathrm{u}_3^2}
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:volumen"/>
| |
| − | Das elementare Volumenelement erhält man durch Multiplikation der Seitenlängen gemäß <xr id="fig:krummlinige_koordinaten2"/>:
| |
| − | :<equation id="eqn:elementar">
| |
| − | <math>
| |
| − | \mathrm{d}V = h_1 h_2 h_3 \mathrm{d}\mathrm{u}_1 \mathrm{d}\mathrm{u}_2 \mathrm{d}\mathrm{u}_3
| |
| − | </math>
| |
| − | </equation>
| |
| − | <xr id="eqn:elementar"/>
| |
Den einfachsten Fall stellt das kartesische Koordinatensystem dar, bei dem die als x-, y- und z-Achse bezeichnet geradlinigen Koordinatenachsen zueinander orthogonal sind. Ihr gemeinsamer Schnittpunkt wird als Koordinatenursprung bzw. direkt als Ursprung bezeichnet. Die Richtung wachsender Koordinatenwerte wird für die Achsen so festgelegt, dass die Einheitsvektoren 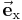 ,
, 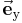 ,
, 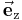 , die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
, die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
Eine Besonderheit beim kartesischen Koordinatensystem besteht darin, dass die Richtung der Einheitsvektoren aufgrund der geradlinigen Koordinaten x, y, z konstant, d. h. unabhängig von deren Position im Raum ist.
Als Koordinatenflächen erhält man die drei orthogonal zueinander angeordneten Ebenen x = const. (entspricht der y-z-Ebene), y = const. (entspricht der x-z-Ebene) und z = const. (entspricht der x-y-Ebene).
wird vektorielles Wegelement genannt. Seine Länge ist durch die Beziehung
gegeben.
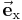 ,
, 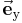 ,
, 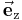 , die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
, die jeweils parallel zu den durch den betreffenden Index gekennzeichneten Koordinatenachsen verlaufen, im Sinne der obigen Gleichung ein Rechtssystem bilden. Dreht man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse, d. h. gegen den Uhrzeigersinn, dann erhält man bei gleichzeitiger Verschiebung in Richtung der positiven z-Achse eine Rechtsschraube.
 der Länge
der Länge 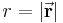 beschrieben:
beschrieben:
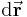 beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz in Richtung der gleichnamigen Koordinaten
beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz in Richtung der gleichnamigen Koordinaten