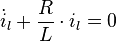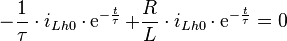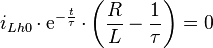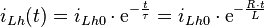Getb:Beispiel für eine DGL 1. Ordnung: Das RL-Glied: Unterschied zwischen den Versionen

Aus GET A
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „==Aufstellen der Differenzialgleichung== ==Lösung der homogenen Differenzialgleichung== Ziel ist es, die eben aufgestellte DGL für das RL-Glied zu lösen. D…“)
 
Zeile 7: Zeile 7:
  
 
Die gesuchte Funktion ist der Verlauf des Stroms <math> i_{Lh}(t) </math>. Zur Lösung wird der Exponentialansatz angesetzt. Der gesuchte Strom <math> i_{Lh}(t) </math> hat die Einheit Ampere, sodass auch die Konstante <math> i_{Lh0} </math> die Einheit Ampere hat, während die Exponentialfunktion einheitenlos ist. Statt mit <math> \lambda </math> wird der Exponentialansatz mit <math> \textstyle \frac{1}{\tau} </math> geschrieben, um den Zusammenhang mit der Zeitkonstante <math> \tau </math> der Schaltung zu verdeutlichen. Der Exponentialansatz und dessen Ableitung lauten für diesen Fall also:
 
Die gesuchte Funktion ist der Verlauf des Stroms <math> i_{Lh}(t) </math>. Zur Lösung wird der Exponentialansatz angesetzt. Der gesuchte Strom <math> i_{Lh}(t) </math> hat die Einheit Ampere, sodass auch die Konstante <math> i_{Lh0} </math> die Einheit Ampere hat, während die Exponentialfunktion einheitenlos ist. Statt mit <math> \lambda </math> wird der Exponentialansatz mit <math> \textstyle \frac{1}{\tau} </math> geschrieben, um den Zusammenhang mit der Zeitkonstante <math> \tau </math> der Schaltung zu verdeutlichen. Der Exponentialansatz und dessen Ableitung lauten für diesen Fall also:
 +
 +
:<math> i_{Lh}(t) = i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} </math>
 +
 +
:<math> \dot i_{Lh}(t) = - \frac{1}{\tau} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} </math>
 +
 +
Beides kann nun in die homogene DGL eingesetzt werden. Es ergibt sich:
 +
 +
:<math> - \frac{1}{\tau} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} + \frac{R}{L} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} = 0 </math>
 +
 +
Zusammenfassen liefert folgenden Ausdruck:
 +
 +
:<math> i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} \cdot \left( \frac{R}{L} - \frac{1}{\tau} \right) = 0 </math>
 +
 +
Diese Gleichung ist erfüllt, wenn einer der Faktoren gleich 0 ist. Die e-Funktion kann niemals null sein. Der Fall <math>i_{Lh0}=0 </math> führt zur Lösung <math> i_{Lh}(t)=0 </math> und ist für die Praxis meist nicht relevant, da sich in diesem Fall der Strom <math> i_L </math> nicht zeitlich ändern würde. Aus <math> \textstyle (\frac{R}{L} - \frac{1}{\tau}) =0 </math> folgt aber <math> \textstyle \frac{R}{L} =  \frac{1}{\tau} \Rightarrow \tau =\frac{L}{R} </math>. Damit wurde die Zeitkonstante der Schaltung bestimmt und die Lösung für die homogene DGL lautet:
 +
 +
:<math> i_{Lh}(t) = i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} = i_{Lh0} \cdot \operatorname{e}^{- \frac{R \cdot t}{L}} </math>
 +
 
==Lösung der inhomogenen Differenzialgleichung==
 
==Lösung der inhomogenen Differenzialgleichung==
  
 
==Anpassung der allgemeinen Lösung an die spezielle Anwendung==
 
==Anpassung der allgemeinen Lösung an die spezielle Anwendung==

Version vom 27. April 2016, 10:11 Uhr

Aufstellen der Differenzialgleichung

Lösung der homogenen Differenzialgleichung

Ziel ist es, die eben aufgestellte DGL für das RL-Glied zu lösen. Die dazugehörige homogene DGL lautet:

\dot i_l + \frac{R}{L} \cdot i_l = 0

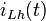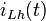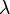Die gesuchte Funktion ist der Verlauf des Stroms i_{Lh}(t) . Zur Lösung wird der Exponentialansatz angesetzt. Der gesuchte Strom i_{Lh}(t) hat die Einheit Ampere, sodass auch die Konstante i_{Lh0} die Einheit Ampere hat, während die Exponentialfunktion einheitenlos ist. Statt mit \lambda wird der Exponentialansatz mit 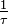\textstyle \frac{1}{\tau} geschrieben, um den Zusammenhang mit der Zeitkonstante 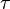\tau der Schaltung zu verdeutlichen. Der Exponentialansatz und dessen Ableitung lauten für diesen Fall also:

i_{Lh}(t) = i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}}
\dot i_{Lh}(t) = - \frac{1}{\tau} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}}

Beides kann nun in die homogene DGL eingesetzt werden. Es ergibt sich:

- \frac{1}{\tau} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} + \frac{R}{L} \cdot i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} = 0

Zusammenfassen liefert folgenden Ausdruck:

i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} \cdot \left( \frac{R}{L} - \frac{1}{\tau} \right) = 0

Diese Gleichung ist erfüllt, wenn einer der Faktoren gleich 0 ist. Die e-Funktion kann niemals null sein. Der Fall 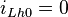i_{Lh0}=0 führt zur Lösung 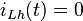i_{Lh}(t)=0 und ist für die Praxis meist nicht relevant, da sich in diesem Fall der Strom 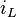i_L nicht zeitlich ändern würde. Aus 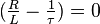\textstyle (\frac{R}{L} - \frac{1}{\tau}) =0 folgt aber 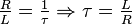\textstyle \frac{R}{L} = \frac{1}{\tau} \Rightarrow \tau =\frac{L}{R} . Damit wurde die Zeitkonstante der Schaltung bestimmt und die Lösung für die homogene DGL lautet:

i_{Lh}(t) = i_{Lh0} \cdot \operatorname{e}^{- \frac{t}{\tau}} = i_{Lh0} \cdot \operatorname{e}^{- \frac{R \cdot t}{L}}

Lösung der inhomogenen Differenzialgleichung

Anpassung der allgemeinen Lösung an die spezielle Anwendung

Abgerufen von „https://getwww.uni-paderborn.de/wiki/geta/index.php?title=Getb:Beispiel_für_eine_DGL_1._Ordnung:_Das_RL-Glied&oldid=6978“