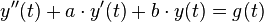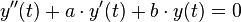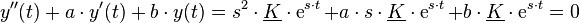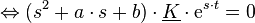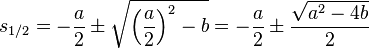Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 2. Ordnung: Unterschied zwischen den Versionen
Getb (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Gegeben sei eine inhomogene, lineare Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten. Diese DGL lässt sich allgemein schreiben als: :<math> y''…“) |
Getb (Diskussion | Beiträge) |
||
| Zeile 25: | Zeile 25: | ||
Zwei linear unabhängige partikuläre Lösungen lassen sich mit Hilfe des komplexen Exponentialansatzes <math> y(t)=\underline{K} \cdot \operatorname{e}^{s \cdot t} </math> finden. Hierbei ist zu beachten, dass mit <math> \underline{K} </math> schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem <math> \underline{K} </math> deutet an, dass <math> \underline{K} </math> komplexe Werte annehmen kann. Auch die Variable <math> s </math> kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass <math> s </math> komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten <math> \underline{K} </math> anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann. | Zwei linear unabhängige partikuläre Lösungen lassen sich mit Hilfe des komplexen Exponentialansatzes <math> y(t)=\underline{K} \cdot \operatorname{e}^{s \cdot t} </math> finden. Hierbei ist zu beachten, dass mit <math> \underline{K} </math> schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem <math> \underline{K} </math> deutet an, dass <math> \underline{K} </math> komplexe Werte annehmen kann. Auch die Variable <math> s </math> kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass <math> s </math> komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten <math> \underline{K} </math> anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann. | ||
| + | |||
| + | Der Exponentialansatz und dessen Ableitungen <math>y'(t)=s \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} </math> und <math>y''(t)=s^2 \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} </math> können nun in die homogene DGL eingesetzt werden: | ||
| + | |||
| + | :<math> y''(t)+a \cdot y'(t)+b \cdot y(t) = s^2 \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} + a \cdot s \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} + b \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} = 0 </math> | ||
| + | |||
| + | :<math> \Leftrightarrow (s^2 + a \cdot s + b) \cdot \underline{K} \cdot \operatorname{e}^{s \cdot t} = 0 </math> | ||
| + | |||
| + | Diese Gleichung ist erfüllt, wenn einer der Faktoren 0 ist. Die e-Funktion kann niemals 0 sein, und der Fall <math>\underline{K}=0 </math> führt zu der trivialen Lösung <math> y=0 </math>. Somit muss der Ausdruck in der Klammer zu Null werden. Die daraus resultierende Bedingung <math> s^2+a \cdot s+b=0 </math> heißt charakteristische Gleichung und kann zum Beispiel mit der p-q-Formel aufgelöst werden: | ||
| + | |||
| + | :<math> s_{1/2} = - \dfrac{a}{2} \pm \sqrt{\left( \dfrac{a}{2} \right)^2 - b} = -\dfrac{a}{2} \pm \dfrac{\sqrt{a^2-4b}}{2} </math> | ||
| + | |||
| + | Die Lösungen <math> s_{1/2} </math> heißen Eigenwerte. Es ergeben sich drei verschiedene Lösungsfälle: | ||
| + | *<math> a^2-4b > 0 </math> → Die charakteristische Gleichung hat zwei verschiedene, reelle Lösungen | ||
| + | |||
| + | *<math> a^2-4b = 0 </math> → Die charakteristische Gleichung hat zwei gleiche, reelle Lösungen | ||
| + | |||
| + | *<math> a^2-4b < 0 </math> → Die charakteristische Gleichung hat zwei zueinander konjugiert komplexe Lösungen (komplexe Lösungen treten stets als konjugiert komplexe Paare auf) | ||
| + | |||
Version vom 24. April 2016, 13:33 Uhr
Gegeben sei eine inhomogene, lineare Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten. Diese DGL lässt sich allgemein schreiben als:
Wobei 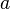 und
und 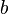 Konstanten sind. Die Lösung erfolgt genauso wie die Lösung einer DGL 1. Ordnung in vier Schritten:
Konstanten sind. Die Lösung erfolgt genauso wie die Lösung einer DGL 1. Ordnung in vier Schritten:
- Lösung der dazugehörigen homogenen DGL
- Finden einer partikulären Lösung der inhomogenen DGL
- Addieren der beiden Lösungen liefert die allgemeine Lösung der inhomogenen DGL
- Berücksichtigung von Anfangsbedingungen
Inhaltsverzeichnis
Lösung der homogenen linearen Differenzialgleichung
Die zur inhomogenen DGL dazugehörige homogene DGL lautet:
Die allgemeine Lösung einer Differenzialgleichung 2. Ordnung enthält zwei Parameter. Im Falle einer linearen DGL 2. Ordnung mit konstanten Koeffizienten ist die allgemeine Lösung eine Linearkombination von zwei linear unabhängigen partikulären Lösungen. Die Koeffizienten der partikulären Lösungen sind die beiden Parameter. Formal gilt dann für die allgemeine Lösung:
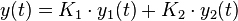 mit
mit 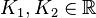 , wobei weiterhin gelten muss:
, wobei weiterhin gelten muss:
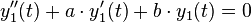 (y1 ist partikuläre Lösung der homogenen DGL)
(y1 ist partikuläre Lösung der homogenen DGL) (y2 ist partikuläre Lösung der homogenen DGL)
(y2 ist partikuläre Lösung der homogenen DGL)-
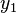 und
und 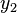 sind linear unabhängig
sind linear unabhängig
Beide Lösungen müssen also die DGL erfüllen und linear unabhängig sein. Allgemein gilt, dass die Lösungen 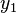 und
und 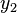 auch komplexwertig sein können.
auch komplexwertig sein können.
Zwei linear unabhängige partikuläre Lösungen lassen sich mit Hilfe des komplexen Exponentialansatzes 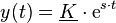 finden. Hierbei ist zu beachten, dass mit
finden. Hierbei ist zu beachten, dass mit 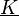 schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem
schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem 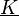 deutet an, dass
deutet an, dass 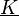 komplexe Werte annehmen kann. Auch die Variable
komplexe Werte annehmen kann. Auch die Variable  kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass
kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass  komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten
komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten 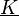 anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann.
anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann.
Der Exponentialansatz und dessen Ableitungen 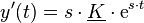 und
und 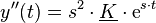 können nun in die homogene DGL eingesetzt werden:
können nun in die homogene DGL eingesetzt werden:
Diese Gleichung ist erfüllt, wenn einer der Faktoren 0 ist. Die e-Funktion kann niemals 0 sein, und der Fall 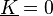 führt zu der trivialen Lösung
führt zu der trivialen Lösung 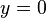 . Somit muss der Ausdruck in der Klammer zu Null werden. Die daraus resultierende Bedingung
. Somit muss der Ausdruck in der Klammer zu Null werden. Die daraus resultierende Bedingung 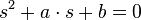 heißt charakteristische Gleichung und kann zum Beispiel mit der p-q-Formel aufgelöst werden:
heißt charakteristische Gleichung und kann zum Beispiel mit der p-q-Formel aufgelöst werden:
Die Lösungen 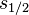 heißen Eigenwerte. Es ergeben sich drei verschiedene Lösungsfälle:
heißen Eigenwerte. Es ergeben sich drei verschiedene Lösungsfälle:
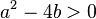 → Die charakteristische Gleichung hat zwei verschiedene, reelle Lösungen
→ Die charakteristische Gleichung hat zwei verschiedene, reelle Lösungen
 → Die charakteristische Gleichung hat zwei gleiche, reelle Lösungen
→ Die charakteristische Gleichung hat zwei gleiche, reelle Lösungen
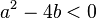 → Die charakteristische Gleichung hat zwei zueinander konjugiert komplexe Lösungen (komplexe Lösungen treten stets als konjugiert komplexe Paare auf)
→ Die charakteristische Gleichung hat zwei zueinander konjugiert komplexe Lösungen (komplexe Lösungen treten stets als konjugiert komplexe Paare auf)