Getb:Allgemeine Hinweise zu Differenzialgleichungen

← Zurück: Getb:Differenzialgleichungen

Übersicht: Allgemeine Hinweise

Vorwärts: Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 1. Ordnung →

Unterschied zwischen Differenzialgleichungen und normalen Gleichungen

Eine Gleichung heißt Differenzialgleichung (DGL), wenn die Ableitungen einer unbekannten, gesuchten Funktion in der Gleichung vorkommen. Die höchste auftretende Ableitung bestimmt dabei die Ordnung der Differenzialgleichung. Neben den Ableitungen können in der Gleichung die Funktion selbst, die Variablen, von denen die Funktion abhängt (sogenannte unabhängige Variablen), und weitere mathematische Ausdrücke vorkommen. Die Lösung der Differenzialgleichung ist die Funktion, welche die Differenzialgleichung erfüllt. Das bedeutet, dass die Gleichung aufgeht, wenn man diese Funktion entsprechend der Differenzialgleichung ableitet und einsetzt.

Beispiel:

$y'''(t)+2 \cdot y'(t)=\cos (t)$

ist eine Differenzialgleichung 3. Ordnung mit der unabhängigen Variable 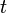$t$. Die Funktion

$y(t)=\sin (t)$

ist eine Lösung der Differenzialgleichung. Dies wird deutlich, wenn die folgenden Ableitungen eingesetzt werden:

$y'(t)=\cos (t)$

$y''(t)=-\sin (t)$

$y'''(t)=-\cos (t)$

Eine „normale“ Gleichung beschreibt den Zusammenhang zwischen dem Funktionswert und einer oder mehrerer Variablen sowie ggf. weiteren Ausdrücken. Eine Differenzialgleichung stellt dagegen im Wesentlichen einen Zusammenhang der Änderungsraten (Ableitungen) einer gesuchten Funktion her.

Gewöhnliche und partielle Differenzialgleichungen

Hängt die gesuchte Funktion nur von einer Variablen ab, z.B. 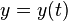$y=y(t)$, spricht man von einer gewöhnlichen Differenzialgleichung. Wenn die gesuchte Funktion von mehreren Variablen abhängt, zum Beispiel $y=y(x_1,x_2,x_3)$ wobei $(x_1,x_2,x_3)$ z.B. die Raumkoordinaten sein können, heißen die Ableitungen der Funktion partielle Ableitungen. Die daraus resultierenden Differenzialgleichungen heißen deshalb partielle Differenzialgleichungen. Partielle Ableitungen und die entsprechenden Differenzialgleichungen werden in der Vorlesung „Höhere Mathematik C“ ausführlicher behandelt.

In der Veranstaltung „Grundlagen der Elektrotechnik B“ werden nur gewöhnliche Differenzialgleichungen behandelt, weshalb im Folgenden immer nur die Abhängigkeit von einer Variablen betrachtet wird.

Lineare Differenzialgleichungen

Lineare Differenzialgleichungen sind eine wichtige Kategorie von Differenzialgleichungen. Eine gewöhnliche lineare Differenzialgleichung n-ter Ordnung lässt sich in folgende Form bringen:

$y^{(n)}(t)+a_{n-1}(t) \cdot y^{(n-1)}(t)+ \cdot \cdot \cdot + a_{1}(t) \cdot y'(t)+a_{0}(t) \cdot y = g(t)$

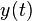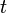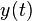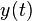Dabei steht $y^{(n)}(t)$ für die n-te Ableitung von $y(t)$. Die Koeffizienten $a(t)$ dürfen explizit die unabhängige Variable $t$ enthalten. Die Funktion $y(t)$ und ihre Ableitungen kommen in linearen Differenzialgleichungen nur in der ersten Potenz vor. In den Koeffizienten $a(t)$ dürfen deshalb die Funktion $y(t)$ und ihre Ableitungen nicht vorkommen, denn Ausdrücke wie $y(t) \cdot y''(t)$ oder $(y''(t))^2$ sind nichtlinear.

Autonomie

Eine Differenzialgleichung heißt autonom, wenn sie nicht explizit von der unabhängigen Variable abhängt. Die Abhängigkeit der DGL von der unabhängigen Variablen darf nur implizit durch die gesuchte Funktion und ihren Ableitungen gegeben sein. Beispiel:

$y''(t)+5=y(t)$

ist eine autonome Differenzialgleichung, da die Abängigkeit von der unabhängigen Variable 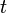$t$ nur implizit durch die Funktion 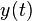$y(t)$ und ihrer Ableitung gegeben ist. Die DGL

$y''(t)=t^2 \cdot y(t)$

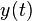ist dagegen keine autonome Differenzialgleichung, da wegen dem Faktor $t^2$ eine explizite Abhängigkeit des Koeffizienten vor $y(t)$ von der unabhängigen Variable 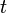$t$ besteht.

Zeitinvarianz

Ein System heißt zeitinvariant, wenn das Verhalten des Systems bei einer zeitlichen Verschiebung des Eingangssignals gleich bleibt. Die Ausgangsgröße zeigt dann, bis auf die zeitliche Verschiebung, das gleiche Verhalten. Ein einfaches Beispiel zur Veranschaulichung:

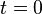An einen Widerstand $R=1\Omega$ wird zum Zeitpunkt $t=0$ eine Spannung von $U=1V$ angelegt. Es stellt sich ab diesem Zeitpunkt ein konstanter Strom von $I=1A$ ein. Wird die gleiche Spannung erst zum Zeitpunkt $t=t_0$ angelegt, stellt sich ab diesem Zeitpunkt auch ein konstanter Strom von $I=1A$ ein. Das Verhalten der Ausgangsgröße ist, bis auf die zeitliche Verschiebung, identisch. Das System ist zeitinvariant.

Nun sei der Widerstand zeitabhängig mit $\textstyle r(t)=1 \Omega + \frac{\Omega}{s} \cdot t$. Wird zum Zeitpunkt 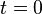$t=0$ eine Spannung von $U=1V$ angelegt, gilt für den Strom zu diesem Zeitpunkt:

$i(t=0)=\frac{U}{r(t=0)}=\frac{1V}{1\Omega}=1A$

Wird erst zum Zeitpunkt $t=t_0$ die Spannung $U$ angelegt, gilt für den Strom zu diesem Zeitpunkt:

$i(t=t_0)=\frac{U}{r(t=t_0)}=\frac{1V}{1\Omega + 1\frac{\Omega}{s} \cdot t_0} \ne 1A$

Das System zeigt also bei gleichem Eingangssignal zu unterschiedlichen Einschaltzeitpunkten ein unterschiedliches Verhalten. Damit ist das System zeitvariant. Der Einfluss der Temperatur, die z.B. als Funktion der Zeit gegeben ist, auf die Leitfähigkeit des Widerstands kann beispielsweise zu einem zeitvarianten Verhalten führen.

Wenn das zeitliche Verhalten eines Systems durch eine lineare autonome Differenzialgleichung beschrieben werden kann, dann ist das System zeitinvariant.

Homogene und inhomogene Differenzialgleichungen

Eine lineare Differenzialgleichung der Form:

$y^{(n)}(t)+a_{n-1}(t) \cdot y^{(n-1)}(t)+ \cdot \cdot \cdot + a_{1}(t) \cdot y'(t)+a_{0}(t) \cdot y = g(t)$

heißt homogen, wenn die Störfunktion $g(t)=0$ ist. In diesem Fall lautet die lineare DGL:

$y^{(n)}(t)+a_{n-1}(t) \cdot y^{(n-1)}(t)+ \cdot \cdot \cdot + a_{1}(t) \cdot y'(t)+a_{0}(t) \cdot y =0$

Wenn $g(t) \ne 0$ gilt, spricht man von einer inhomogenen Differenzialgleichung. Wird die Störfunktion einer inhomogenen linearen DGL gleich 0 gesetzt, erhält man die zur Differenzialgleichung zugehörige homogene DGL.

Generell gilt, dass die homogene DGL das Eigenverhalten eines dynamischen Systems unter Berücksichtigung der Anfangswerte beschreibt. Die Störfunktion beschreibt eine äußere Einflussgröße auf das System. Die inhomogene DGL beschreibt die Wechselwirkung zwischen der Eigendynamik des Systems und der äußeren Einflussgröße.

Bei elektrischen Netzwerken beschreibt beispielsweise die homogene DGL das Systemverhalten einer Schaltung aus Widerständen, Spulen und Kondensatoren ohne äußere Einflüsse wie Spannungs- und Stromquellen oder ähnliche Elemente, jedoch in Abhängigkeit der Anfangswerte der Spulenströme und Kondensatorspannungen. Dies stellt die Eigendynamik des Systems dar. Mit der Störfunktion wird der äußere Einfluss durch zusätzliche Spannungs- und Stromquellen oder ähnliche Elemente berücksichtigt. Die inhomogene DGL beschreibt demnach die Wechselwirkung zwischen der Eigendynamik der Schaltung und der Anregung durch eingeprägte Ströme und/oder Spannungen.

Vorgehen bei der Lösung von Differenzialgleichungen

Eine Funktion 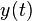$y(t)$ heißt Lösung der DGL, wenn sie mit ihren Ableitungen die Gleichung erfüllt. Man muss zwischen der allgemeinen Lösung und einer speziellen (partikulären) Lösung der Differenzialgleichung unterscheiden. Die allgemeine Lösung einer Differenzialgleichung n-ter Ordnung enthält noch n voneinander unabhängige Parameter. Eine spezielle Lösung ist, wie der Name schon andeutet, ein Spezialfall der allgemeinen Lösung mit konkreten Werten für die n Parameter. Diese konkreten Werte ergeben sich für eine spezielle Anwendung aus gegebenen Randbedingungen und Anfangswerten.

Es gibt kein allgemeingültiges Lösungsverfahren für alle Differenzialgleichungen. Je nach Typ der Differenzialgleichung muss ein anderer Ansatz gewählt werden, bei komplexeren Gleichungen kann häufig nur ein numerisches Lösungsverfahren angewandt werden.

Einige Möglichkeiten zur Lösung sind:

• Integration (bei einfachen DGLen)
• Trennung der Variablen (bei einigen DGLen 1. Ordnung)
• Exponentialansatz (bei einigen linearen DGLen)
• Substitution
• Überlagerung von Lösungen

In der Veranstaltung GET B werden nur lineare Differenzialgleichungen 1. und 2. Ordnung für die Beschreibung der behandelten elektrischen Netzwerke gebraucht. Für die Lösung dieser DGLen sind im Allgemeinen folgende Schritte notwendig:

1. Allgemeine Lösung $y_{h}(t)$ der zugehörigen homogenen DGL bestimmen
2. Eine partikuläre Lösung $y_{p}(t)$ der inhomogenen DGL finden
3. Die allgemeine Lösung der inhomogenen DGL ergibt sich dann durch Überlagerung (Superposition) beider Lösungen: $y(t)=y_{h}(t)+y_{p}(t)$

In den nachfolgenden Artikeln wird ausführlicher auf die Lösung von linearen Differenzialgleichungen 1. und 2. Ordnung mit konstanten Koeffizienten eingegangen.