Homogeneous coordinates
| ← Back: Rotation | Overview: Transformations | Next: Combinations of transformations → |
In this article three-dimensional space is regarded because it is usually used in robotics. Rotation of three-dimensional coordinates can be described by an 3-by-3 matrix. All the components of the matrix are multiplied with one of the three coordinates. So the transformation is dependent on the original coordinates. Translation however is actually a vector addition and so independent of the original coordinates (see subarticle about translation).
To be able to also apply a translation by matrix multiplication, an additional dimension is introduced. For vectors, the additional fourth component is always 1. So a three-dimensional vector 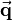 in homogeneous coordinates looks a sfollows:
in homogeneous coordinates looks a sfollows:
A homogeneous transformation matrix 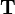 for three-dimensional space is a 4-by-4 matrix.
for three-dimensional space is a 4-by-4 matrix. 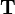 consists of the 3-by-3 rotation matrix
consists of the 3-by-3 rotation matrix 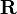 and a 3-by-1 translation vector
and a 3-by-1 translation vector 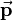 combined with the last row of the identity matrix:
combined with the last row of the identity matrix:
Let the components of the rotation matrix 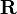 and the translation vector
and the translation vector 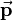 be denoted as follows:
be denoted as follows:
So the multiplication of a homogeneous transformation matrix 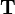 with a vector
with a vector 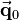 in homogeneous coordinates leads to:
in homogeneous coordinates leads to:
As can be seen in the resulting vector, the components  and
and  are independent of the original coordinates and just added to the x- or the y-coordinate, respectively.
are independent of the original coordinates and just added to the x- or the y-coordinate, respectively.
![\vec{\mathbf{q}}=
\left[\begin{array}{c}
q_x\\
q_y\\
q_z\\
1
\end{array}\right]](/wiki/robotics/images/math/a/f/2/af2bf65605bc6259cd307e3d9d01f7ab.png)
![\mathbf{T}=
\left[\begin{array}{ccc|c}
& & & \\
& \mathbf{R} & & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/1/3/2/1327593f05795df92e5c12f1a1a27f84.png)
![\mathbf{R}=
\left[\begin{array}{ccc}
r_{11} & r_{12} & r_{13}\\
r_{21} & r_{22} & r_{23}\\
r_{31} & r_{32} & r_{33}
\end{array}\right], \qquad
\vec{\mathbf{p}}=
\left[\begin{array}{c}
p_x\\
p_y\\
p_z
\end{array}\right]](/wiki/robotics/images/math/3/9/7/3979b48a22707b24e81069e63f9bb307.png)
![\vec{\mathbf{q}}_1=
\left[\begin{array}{c}
x_1\\
y_1\\
z_1\\
1
\end{array}\right]=
\mathbf{T} \cdot \vec{\mathbf{q}}_0 =
\left[\begin{array}{cccc}
r_{11} & r_{12} & r_{13} & p_x\\
r_{21} & r_{22} & r_{23} & p_y\\
r_{31} & r_{32} & r_{33} & p_z\\
0 & 0 & 0 & 1
\end{array}\right] \cdot
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right]=
\left[\begin{array}{ccc}
t_{11} & t_{12} & t_{13}\\
t_{21} & t_{22} & t_{23}\\
0 & 0 & 1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
t_{11}\cdot x_0+t_{12}\cdot y_0+t_{13}\cdot 1\\
t_{21}\cdot x_0+t_{22}\cdot y_0+t_{23}\cdot 1\\
0\cdot x_0+0\cdot y_0+1\cdot1
\end{array}\right]=
\left[\begin{array}{c}
t_{11}\cdot x_0+t_{12}\cdot y_0+{\color{Green}\mathbf{t_{13}}}\\
t_{21}\cdot x_0+t_{22}\cdot y_0+{\color{Green}\mathbf{t_{23}}}\\
1
\end{array}\right]](/wiki/robotics/images/math/c/f/3/cf3980b93a2e6a51d4061fc8941398d0.png)