Difference between revisions of "Homogeneous coordinates"
| (29 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Navigation|before=[[Rotation]]|overview=[[Transformations]]|next=[[Combinations of transformations]]}} | {{Navigation|before=[[Rotation]]|overview=[[Transformations]]|next=[[Combinations of transformations]]}} | ||
| − | [[Rotation]] of | + | In this article three-dimensional space is regarded because it is usually used in robotics. [[Rotation]] of three-dimensional coordinates can be described by a 3-by-3 matrix. All the components of the matrix are multiplied with one of the three coordinates. So the transformation is dependent on the original coordinates. Translation however is actually a [[Simple arithmetic operations|vector addition]] and so independent of the original coordinates (see subarticle about [[Translation|translation]]). |
| − | To be able to also apply a translation by [[Multiplication of matrices|matrix multiplication]], an additional dimension is introduced. For three-dimensional | + | To be able to also apply a translation by [[Multiplication of matrices|matrix multiplication]], an additional dimension is introduced. For vectors, the additional fourth component is always 1. So a three-dimensional vector <math>\vec{\mathbf{q}}</math> in homogeneous coordinates looks as follows: <br/> |
| + | :<math> | ||
| + | \vec{\mathbf{q}}= | ||
| + | \left[\begin{array}{c} | ||
| + | q_x\\ | ||
| + | q_y\\ | ||
| + | q_z\\ | ||
| + | 1 | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | |||
| + | A homogeneous transformation matrix <math>\mathbf{T}</math> for three-dimensional space is a 4-by-4 matrix. <math>\mathbf{T}</math> consists of a 3-by-3 rotation matrix <math>\mathbf{R}</math> and a 3-by-1 translation vector <math>\vec{\mathbf{p}}</math> combined with the last row of the identity matrix:<br/> | ||
:<math> | :<math> | ||
\mathbf{T}= | \mathbf{T}= | ||
| Line 11: | Line 22: | ||
& & & \\ \hline | & & & \\ \hline | ||
0 & 0 & 0 & 1 | 0 & 0 & 0 & 1 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\end{array}\right] | \end{array}\right] | ||
</math> | </math> | ||
| − | + | Let the components of the rotation matrix <math>\mathbf{R}</math> and the translation vector <math>\vec{\mathbf{p}}</math> be denoted as follows:<br/> | |
| + | :<math> | ||
| + | \mathbf{R}= | ||
| + | \left[\begin{array}{ccc} | ||
| + | r_{11} & r_{12} & r_{13}\\ | ||
| + | r_{21} & r_{22} & r_{23}\\ | ||
| + | r_{31} & r_{32} & r_{33} | ||
| + | \end{array}\right], \qquad | ||
| + | \vec{\mathbf{p}}= | ||
| + | \left[\begin{array}{c} | ||
| + | p_x\\ | ||
| + | p_y\\ | ||
| + | p_z | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | |||
| + | So the multiplication of a homogeneous transformation matrix <math>\mathbf{T}</math> with a vector <math>\vec{\mathbf{q}}_0</math> in homogeneous coordinates leads to:<br/> | ||
:<math> | :<math> | ||
| + | \vec{\mathbf{q}}_1= | ||
\left[\begin{array}{c} | \left[\begin{array}{c} | ||
x_1\\ | x_1\\ | ||
y_1\\ | y_1\\ | ||
| + | z_1\\ | ||
1 | 1 | ||
\end{array}\right]= | \end{array}\right]= | ||
| − | \mathbf{T} \cdot | + | \mathbf{T} \cdot \vec{\mathbf{q}}_0 = |
| + | \left[\begin{array}{cccc} | ||
| + | r_{11} & r_{12} & r_{13} & p_x\\ | ||
| + | r_{21} & r_{22} & r_{23} & p_y\\ | ||
| + | r_{31} & r_{32} & r_{33} & p_z\\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] \cdot | ||
\left[\begin{array}{c} | \left[\begin{array}{c} | ||
x_0\\ | x_0\\ | ||
y_0\\ | y_0\\ | ||
| + | z_0\\ | ||
1 | 1 | ||
\end{array}\right]= | \end{array}\right]= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\left[\begin{array}{c} | \left[\begin{array}{c} | ||
| − | + | r_{11}\cdot x_0+r_{12}\cdot y_0+r_{13}\cdot z_0+\mathbf{p_x}\\ | |
| − | + | r_{21}\cdot x_0+r_{22}\cdot y_0+r_{23}\cdot z_0+\mathbf{p_y}\\ | |
| − | + | r_{31}\cdot x_0+r_{32}\cdot y_0+r_{33}\cdot z_0+\mathbf{p_z}\\ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
1 | 1 | ||
\end{array}\right] | \end{array}\right] | ||
</math> | </math> | ||
| − | As can be seen in the resulting vector, the components <math> | + | As can be seen in the resulting vector, the first 3 summands of each component belong to the rotational part while the components of the translation vector are added independently of the previous coordinates. So in homogeneous coordinates rotation and translation can be performed with a single transformation matrix. The rotation is applied first and then the translation vector is added. Regarding the particular transformations multiplication with a homogeneous transformation matrix is equivalent in cartesian coordinates to multiplication of the input vector by <math>\mathbf{R}</math> and then adding the translation vector:<br/> |
| + | :<math> | ||
| + | \vec{\mathbf{q}}_1= | ||
| + | \mathbf{T} \cdot \vec{\mathbf{q}}_0 \equiv | ||
| + | \mathbf{R}\cdot \vec{\mathbf{q}}_0 + \vec{\mathbf{p}} | ||
| + | </math> | ||
| + | |||
| + | Transformations are applied to one coordinate frame with respect to another certain reference frame. The following notation is used to determine the transformation of the coordinate frame <math>N</math> with respect to the reference frame <math>R</math>: | ||
| + | :<math> | ||
| + | ^R\mathbf{T}_N | ||
| + | </math> | ||
| + | |||
| + | More information about the [[Combinations of transformations|combination of transformations]] and about their order is provided in the following subarticle. | ||
| + | |||
| + | A simple three-dimensional translation in homogeneous coordinates is denoted as follows:<br/> | ||
| + | :<math> | ||
| + | \mathbf{Trans}(p_x,p_y,p_z)= | ||
| + | \left[\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & p_x\\ | ||
| + | 0 & 1 & 0 & p_y\\ | ||
| + | 0 & 0 & 1 & p_z\\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | The matrices introduced for [[Rotation|rotation]] are the following in homogeneous coordinates:<br/> | ||
| + | :<math> | ||
| + | \mathbf{Rot}(x,\varphi)= | ||
| + | \left[\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & 0\\ | ||
| + | 0 & \cos\varphi & -\sin\varphi & 0\\ | ||
| + | 0 & \sin\varphi & \cos\varphi & 0\\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | </math><br/><br/> | ||
| + | :<math> | ||
| + | \mathbf{Rot}(y,\varphi)= | ||
| + | \left[\begin{array}{cccc} | ||
| + | \cos\varphi & 0 & \sin\varphi & 0\\ | ||
| + | 0 & 1 & 0 & 0\\ | ||
| + | -\sin\varphi & 0 & \cos\varphi & 0\\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | </math><br/><br/> | ||
| + | :<math> | ||
| + | \mathbf{Rot}(z,\varphi)= | ||
| + | \left[\begin{array}{cccc} | ||
| + | \cos\varphi & -\sin\varphi & 0 & 0\\ | ||
| + | \sin\varphi & \cos\varphi & 0 & 0\\ | ||
| + | 0 & 0 & 1 & 0\\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | |||
| + | |||
[[Category:Article]] | [[Category:Article]] | ||
[[Category:Transformations]] | [[Category:Transformations]] | ||
Latest revision as of 16:36, 23 October 2015
| ← Back: Rotation | Overview: Transformations | Next: Combinations of transformations → |
In this article three-dimensional space is regarded because it is usually used in robotics. Rotation of three-dimensional coordinates can be described by a 3-by-3 matrix. All the components of the matrix are multiplied with one of the three coordinates. So the transformation is dependent on the original coordinates. Translation however is actually a vector addition and so independent of the original coordinates (see subarticle about translation).
To be able to also apply a translation by matrix multiplication, an additional dimension is introduced. For vectors, the additional fourth component is always 1. So a three-dimensional vector 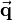 in homogeneous coordinates looks as follows:
in homogeneous coordinates looks as follows:
A homogeneous transformation matrix  for three-dimensional space is a 4-by-4 matrix.
for three-dimensional space is a 4-by-4 matrix.  consists of a 3-by-3 rotation matrix
consists of a 3-by-3 rotation matrix  and a 3-by-1 translation vector
and a 3-by-1 translation vector 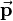 combined with the last row of the identity matrix:
combined with the last row of the identity matrix:
Let the components of the rotation matrix  and the translation vector
and the translation vector 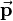 be denoted as follows:
be denoted as follows:
So the multiplication of a homogeneous transformation matrix  with a vector
with a vector 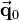 in homogeneous coordinates leads to:
in homogeneous coordinates leads to:
As can be seen in the resulting vector, the first 3 summands of each component belong to the rotational part while the components of the translation vector are added independently of the previous coordinates. So in homogeneous coordinates rotation and translation can be performed with a single transformation matrix. The rotation is applied first and then the translation vector is added. Regarding the particular transformations multiplication with a homogeneous transformation matrix is equivalent in cartesian coordinates to multiplication of the input vector by  and then adding the translation vector:
and then adding the translation vector:
Transformations are applied to one coordinate frame with respect to another certain reference frame. The following notation is used to determine the transformation of the coordinate frame 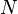 with respect to the reference frame
with respect to the reference frame 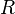 :
:
More information about the combination of transformations and about their order is provided in the following subarticle.
A simple three-dimensional translation in homogeneous coordinates is denoted as follows:
The matrices introduced for rotation are the following in homogeneous coordinates:
![\vec{\mathbf{q}}=
\left[\begin{array}{c}
q_x\\
q_y\\
q_z\\
1
\end{array}\right]](/wiki/robotics/images/math/a/f/2/af2bf65605bc6259cd307e3d9d01f7ab.png)
![\mathbf{T}=
\left[\begin{array}{ccc|c}
& & & \\
& \mathbf{R} & & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/1/3/2/1327593f05795df92e5c12f1a1a27f84.png)
![\mathbf{R}=
\left[\begin{array}{ccc}
r_{11} & r_{12} & r_{13}\\
r_{21} & r_{22} & r_{23}\\
r_{31} & r_{32} & r_{33}
\end{array}\right], \qquad
\vec{\mathbf{p}}=
\left[\begin{array}{c}
p_x\\
p_y\\
p_z
\end{array}\right]](/wiki/robotics/images/math/3/9/7/3979b48a22707b24e81069e63f9bb307.png)
![\vec{\mathbf{q}}_1=
\left[\begin{array}{c}
x_1\\
y_1\\
z_1\\
1
\end{array}\right]=
\mathbf{T} \cdot \vec{\mathbf{q}}_0 =
\left[\begin{array}{cccc}
r_{11} & r_{12} & r_{13} & p_x\\
r_{21} & r_{22} & r_{23} & p_y\\
r_{31} & r_{32} & r_{33} & p_z\\
0 & 0 & 0 & 1
\end{array}\right] \cdot
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
r_{11}\cdot x_0+r_{12}\cdot y_0+r_{13}\cdot z_0+\mathbf{p_x}\\
r_{21}\cdot x_0+r_{22}\cdot y_0+r_{23}\cdot z_0+\mathbf{p_y}\\
r_{31}\cdot x_0+r_{32}\cdot y_0+r_{33}\cdot z_0+\mathbf{p_z}\\
1
\end{array}\right]](/wiki/robotics/images/math/1/9/7/1976c9cc3d0f30fd46c6662a4ee607bb.png)
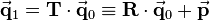
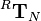
![\mathbf{Trans}(p_x,p_y,p_z)=
\left[\begin{array}{cccc}
1 & 0 & 0 & p_x\\
0 & 1 & 0 & p_y\\
0 & 0 & 1 & p_z\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/d/e/f/defa9b93c084e6bf92f97b4623f134e0.png)
![\mathbf{Rot}(x,\varphi)=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & \cos\varphi & -\sin\varphi & 0\\
0 & \sin\varphi & \cos\varphi & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/5/4/a/54aca09293fbcd0c997358ef9beac8ca.png)
![\mathbf{Rot}(y,\varphi)=
\left[\begin{array}{cccc}
\cos\varphi & 0 & \sin\varphi & 0\\
0 & 1 & 0 & 0\\
-\sin\varphi & 0 & \cos\varphi & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/3/2/b/32bd1a753080c5a5cbdda185ef04252c.png)
![\mathbf{Rot}(z,\varphi)=
\left[\begin{array}{cccc}
\cos\varphi & -\sin\varphi & 0 & 0\\
\sin\varphi & \cos\varphi & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/8/3/0/8304e6d305be0aaf12286f393e7f90db.png)