Difference between revisions of "Quaternions"
| Line 5: | Line 5: | ||
Quaternions avoid these problems. They are an extension of real numbers to a four-dimensional number system using imaginary units. As quaternions have been described at first by William Rowan Hamilton, they are also called ''Hamilton numbers''. | Quaternions avoid these problems. They are an extension of real numbers to a four-dimensional number system using imaginary units. As quaternions have been described at first by William Rowan Hamilton, they are also called ''Hamilton numbers''. | ||
| − | A quaternion consists of a ''scalar part'' with one component and a ''vector part'' with three components. The vector components are assigned to imaginary units, which is why they are also called the ''imaginary part''. A quaternion <math> | + | A quaternion consists of a ''scalar part'' with one component and a ''vector part'' with three components. The vector components are assigned to imaginary units, which is why they are also called the ''imaginary part''. A quaternion <math>q</math> can be written as |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | + | q &= s + \mathbf{v} \\ | |
&= s + v_1i + v_2j + v_3k \\ | &= s + v_1i + v_2j + v_3k \\ | ||
| − | &= | + | &= \text{Re}(q) + \text{Im}(q) |
\end{align} | \end{align} | ||
</math> | </math> | ||
where <math>s, v_1, v_2, v_3 \in \R </math> and <math>i, j, k</math> are imaginary units. | where <math>s, v_1, v_2, v_3 \in \R </math> and <math>i, j, k</math> are imaginary units. | ||
| − | Often the four components of a quaternion are named correspondingly to the label of the quaternion itself. So assuming a quaternion <math> | + | Often the four components of a quaternion are named correspondingly to the label of the quaternion itself. So assuming a quaternion <math>q</math> the four components are also denoted with <math>q</math>: |
:<math> | :<math> | ||
| − | + | q = q_0 + q_1i + q_2j + q_3k | |
</math> | </math> | ||
There is a second notation for quaternions avoiding imaginary units. In this notation the operator <math>\oplus</math> concatenates the scaler and the vector part, which obviously cannot be added to each other. So on one side of the operator there is only the scalar part and on the other side only the vector part: | There is a second notation for quaternions avoiding imaginary units. In this notation the operator <math>\oplus</math> concatenates the scaler and the vector part, which obviously cannot be added to each other. So on one side of the operator there is only the scalar part and on the other side only the vector part: | ||
:<math> | :<math> | ||
| − | + | q = s \oplus \vec{\mathbf{v}} \quad \text{with } \vec{\mathbf{v}} = [v_1, v_2, v_3]^T \in \R^3 | |
</math> | </math> | ||
Revision as of 16:48, 28 May 2015
| ← Back: Euler angles | Overview: Quaternions | Next: Basic properties of quaternions → |
Using homogeneous matrices for transformations is working well in theory. But practically there are several problems especially when multiple transformations are applied successively. First problem is, that matrix multiplication needs a lot of computations and thus computation time. Additionally no computer calculates a hundred percent correctly. So errors in matrix multiplication increase over time when multiple multiplications are calculated. This leads to matrices that are no longer orthonormal, which means that the three coordinate axes described by the matrix are not orthogonal anymore. So applying these matrices results in distorted transformations.
Quaternions avoid these problems. They are an extension of real numbers to a four-dimensional number system using imaginary units. As quaternions have been described at first by William Rowan Hamilton, they are also called Hamilton numbers.
A quaternion consists of a scalar part with one component and a vector part with three components. The vector components are assigned to imaginary units, which is why they are also called the imaginary part. A quaternion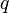 
can be written as
where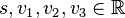 
and 
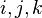are imaginary units.
Often the four components of a quaternion are named correspondingly to the label of the quaternion itself. So assuming a quaternion 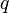the four components are also denoted with :
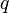There is a second notation for quaternions avoiding imaginary units. In this notation the operator 
concatenates the scaler and the vector part, which obviously cannot be added to each other. So on one side of the operator there is only the scalar part and on the other side only the vector part:
![q = s \oplus \vec{\mathbf{v}} \quad \text{with } \vec{\mathbf{v}} = [v_1, v_2, v_3]^T \in \R^3](/wiki/robotics/images/math/6/4/c/64cacf4835693a3a13a18e7ca90b092d.png)
In the following subarticles all important aspects of quaternions are treated in detail:
