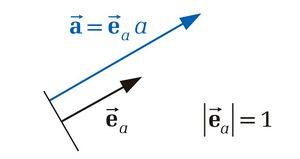
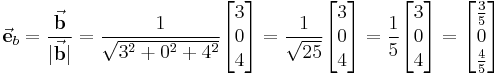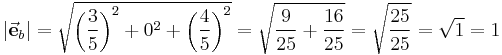Einheitsvektoren
Unter einem Einheitsvektor versteht man allgemein einen Vektor mit dem Betrag beziehungsweise der Länge 1. Der Einheitsvektor 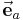 zu einem gegebenen Vektor
zu einem gegebenen Vektor  lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag
lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag 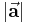 dividiert:
dividiert:
Der Vektor 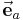 hat die Länge 1 (es gilt also
hat die Länge 1 (es gilt also 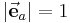 ) und zeigt in Richtung des Vektors
) und zeigt in Richtung des Vektors  . Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag (also einer skalarwertigen Größe) und dem dazugehörigen Einheitsvektor angeben. Der Vektor
. Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag (also einer skalarwertigen Größe) und dem dazugehörigen Einheitsvektor angeben. Der Vektor  kann somit auch wie folgt dargestellt werden:
kann somit auch wie folgt dargestellt werden:
Beobachtet man die Wirkung von Ladungen aufeinander, so lässt sich feststellen, dass diese Kräfte aufeinander ausüben. Werden nun zwei Punktladungen |
Gegeben sei der Vektor Das dieser Vektor tatsächlich die Länge 1 hat, lässt sich leicht durch die Bestimmung des Betrags überprüfen: |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Anthony Croft and Robert Davison, Mathematics for Engineers: a modern interactive approach, 3. Auflage (Pearson-Prentice Hall, 2008)
| ← Zurück: Einführung in die Vektorrechnung | Übersicht: Vektorrechnung | Vorwärts: Einfache Rechenoperationen mit Vektoren → |
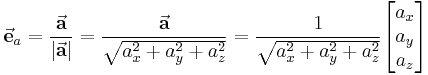
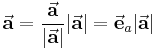
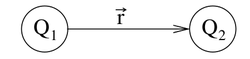
 und
und  im Abstand
im Abstand 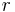 zueinander positioniert (siehe Abbildung), so herrscht zwischen ihnen eine Kradt
zueinander positioniert (siehe Abbildung), so herrscht zwischen ihnen eine Kradt 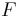 gemäß dem Coulombschen Gesetz:
gemäß dem Coulombschen Gesetz:
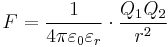
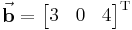 (das
(das 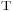 steht für
steht für