Das Flächenintegral: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
| − | In vielen Fällen interessiert es nicht nur, welchen Betrag eine Integration über eine ''Kontur'' ergibt, sondern über eine ganze ''Fläche'' ('''Fragwürdige Aussage'''). Um die Problematik zu veranschaulichen, kann man zunächst ein Wasserrohr betrachten. Die Fläche des Rohres dient als begrenzender Parameter für den maximalen Durchsatz, also wieviel Wasser pro Zeit maximal hindurchfließen kann ('''Plausibilität? Je höher der Druck, desto mehr Wasser geht doch auch hindurch. Warum sollte die Fläche hier begrenzend wirken?'''). Hat man also ein Wasserrohr mit relativ kleinem Querschnitt, so wird weniger Wasser pro Zeit hindurchfließen können als bei einem Rohr mit größerem Querschnitt. Außerdem sollte man berücksichtigen, dass das Wasser in der Mitte des Rohres unter Umständen schneller strömen kann als am Rand, welches einem inhomogenem Durchsatz der Fläche entspricht. Analog zu dem Wasserrohr kann man sich auch ein stromdurchflossenes Kabel vorstellen ('''oder den magnetischen Fluss durch eine Leiterschleife'''). Auch der maximale Stromdurchsatz wird durch die Fläche des Kabels begrenzt ('''falsch!!!'''). Durch materialabhängige Unterschiede kann es zu unterschiedlichen Leitfähigkeiten im Kabel kommen, dies würde einem inhomogenen Durchsatz entsprechen ('''unverständlich'''). Damit diese Faktoren geeignet berücksichtigt werden können, verwendet man bei solchen Beispielen das Flächenintegral, da hier auch gekrümmte Flächen und inhomogene Durchsätze betrachtet werden können. | + | In vielen Fällen interessiert es nicht nur, welchen Betrag eine Integration über eine ''Kontur'' ergibt, sondern über eine ganze ''Fläche'' ('''Fragwürdige Aussage'''). Um die Problematik zu veranschaulichen, kann man zunächst ein Wasserrohr betrachten. Die Fläche des Rohres dient als begrenzender Parameter für den maximalen Durchsatz, also wieviel Wasser pro Zeit maximal hindurchfließen kann ('''Plausibilität? Je höher der Druck, desto mehr Wasser geht doch auch hindurch. Warum sollte die Fläche hier begrenzend wirken?'''). Hat man also ein Wasserrohr mit relativ kleinem Querschnitt, so wird weniger Wasser pro Zeit hindurchfließen können als bei einem Rohr mit größerem Querschnitt. Außerdem sollte man berücksichtigen, dass das Wasser in der Mitte des Rohres unter Umständen schneller strömen kann als am Rand, welches einem inhomogenem Durchsatz der Fläche entspricht. Analog zu dem Wasserrohr kann man sich auch ein stromdurchflossenes Kabel vorstellen ('''oder den magnetischen Fluss durch eine Leiterschleife'''). Auch der maximale Stromdurchsatz wird durch die Fläche des Kabels begrenzt ('''falsch!!!'''). Durch materialabhängige Unterschiede kann es zu unterschiedlichen Leitfähigkeiten im Kabel kommen, dies würde einem inhomogenen Durchsatz entsprechen ('''unverständlich'''). Damit diese Faktoren geeignet berücksichtigt werden können, verwendet man bei solchen Beispielen das Flächenintegral, da hier auch gekrümmte Flächen und inhomogene Durchsätze betrachtet werden können. Argumentationskette besser wie folgt: '''Möchte man den Durchsatz durch eine beliebige Fläche berechnen -> Verwendung des Linienintegrals'''. |
[[Image:Erweiterung_der_integralrechnung_Fluss.jpg|300px|thumb|<caption>Fluss durch eine ebene Fläche</caption>]] | [[Image:Erweiterung_der_integralrechnung_Fluss.jpg|300px|thumb|<caption>Fluss durch eine ebene Fläche</caption>]] | ||
Version vom 24. Juli 2012, 20:31 Uhr
To-do:
- Ausführung von Mehrfachintegralen (Integrationsreihenfolge usw.) ausführlicher beschreiben, ggf. eigenen Abschnitt einfügen
- "Vor das Integral schreiben" statt ziehen
- Einleitung plausibler!!!
In vielen Fällen interessiert es nicht nur, welchen Betrag eine Integration über eine Kontur ergibt, sondern über eine ganze Fläche (Fragwürdige Aussage). Um die Problematik zu veranschaulichen, kann man zunächst ein Wasserrohr betrachten. Die Fläche des Rohres dient als begrenzender Parameter für den maximalen Durchsatz, also wieviel Wasser pro Zeit maximal hindurchfließen kann (Plausibilität? Je höher der Druck, desto mehr Wasser geht doch auch hindurch. Warum sollte die Fläche hier begrenzend wirken?). Hat man also ein Wasserrohr mit relativ kleinem Querschnitt, so wird weniger Wasser pro Zeit hindurchfließen können als bei einem Rohr mit größerem Querschnitt. Außerdem sollte man berücksichtigen, dass das Wasser in der Mitte des Rohres unter Umständen schneller strömen kann als am Rand, welches einem inhomogenem Durchsatz der Fläche entspricht. Analog zu dem Wasserrohr kann man sich auch ein stromdurchflossenes Kabel vorstellen (oder den magnetischen Fluss durch eine Leiterschleife). Auch der maximale Stromdurchsatz wird durch die Fläche des Kabels begrenzt (falsch!!!). Durch materialabhängige Unterschiede kann es zu unterschiedlichen Leitfähigkeiten im Kabel kommen, dies würde einem inhomogenen Durchsatz entsprechen (unverständlich). Damit diese Faktoren geeignet berücksichtigt werden können, verwendet man bei solchen Beispielen das Flächenintegral, da hier auch gekrümmte Flächen und inhomogene Durchsätze betrachtet werden können. Argumentationskette besser wie folgt: Möchte man den Durchsatz durch eine beliebige Fläche berechnen -> Verwendung des Linienintegrals.
Im Gegensatz zum Linienintegral wird beim Flächenintegral die Funktion nicht nur von einer Integrationsvariable bestimmt, sondern von zweien. Alternativ zur ersten Schreibweise
kann für das Flächenintegral auch diese Schreibweise verwendet werden:
Allerdings wird die zweite Schreibweise hier weniger Verwendung finden.
Es wird generell zwischen einem skalaren und einem vektoriellen Flächenintegral unterschieden, je nach Form des Integranden. Bei einem vektoriellen Flächenintegral muss, ähnlich wie beim Linienintegral, das Skalarprodukt gebildet werden:
Während die Richtung der Funktion meist durch die Aufgabe gegeben ist, muss bei der Fläche die Flächennormale bestimmt werden. Dazu wird ein Einheitsvektor 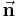 verwendet, der senkrecht auf der Fläche A steht. So erhält die Fläche die Richtung
verwendet, der senkrecht auf der Fläche A steht. So erhält die Fläche die Richtung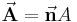 .
Nun nimmt man die Funktion, die einen Fluss oder eine Flussdichte darstellt (im oberen Beispiel wäre das etwa die Wasserdichte, die pro Zeiteinheit durch das Rohr strömt oder man wählt ein eher elektrotechnisches Beispiel wie die magnetische Flussdichte im Durchflutungssatz) und bildet das Skalarprodukt zwischen dem gerichteten Fluss und der Flächennormale.
.
Nun nimmt man die Funktion, die einen Fluss oder eine Flussdichte darstellt (im oberen Beispiel wäre das etwa die Wasserdichte, die pro Zeiteinheit durch das Rohr strömt oder man wählt ein eher elektrotechnisches Beispiel wie die magnetische Flussdichte im Durchflutungssatz) und bildet das Skalarprodukt zwischen dem gerichteten Fluss und der Flächennormale.
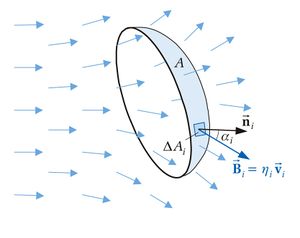
Ist die Fläche A gebogen und die Dichte ortsabhängig, wird sie in viele Teilstücke 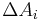 mit i=1,...n unterteilt, sodass die Krümmung dieser Teilstücke vernachlässigt werden kann (vgl. Infinitesimale Volumenelemente). Da man nun keine einheitliche Normale mehr hat, muss für jedes Flächenstück die Flächennormale
mit i=1,...n unterteilt, sodass die Krümmung dieser Teilstücke vernachlässigt werden kann (vgl. Infinitesimale Volumenelemente). Da man nun keine einheitliche Normale mehr hat, muss für jedes Flächenstück die Flächennormale 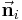 bestimmt werden. Idealerweise kann man sich die Flächenstücke als kleine ebene Teilflächen vorstellen. Anschließend wird analog zum vektoriellem Linienintegral ein Punkt
bestimmt werden. Idealerweise kann man sich die Flächenstücke als kleine ebene Teilflächen vorstellen. Anschließend wird analog zum vektoriellem Linienintegral ein Punkt 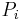 auf der Fläche gewählt und der dazugehörige Funktionswert
auf der Fläche gewählt und der dazugehörige Funktionswert 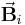 für dieses Flächenstück bestimmt. Nun bildet man das Skalarprodukt zwischen der jeweiligen Flächennormalen und dem Funktionswert.
für dieses Flächenstück bestimmt. Nun bildet man das Skalarprodukt zwischen der jeweiligen Flächennormalen und dem Funktionswert.
Dabei muss der Winkel 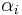 zwischen den Funktionsparametern und der Flächennormalen betrachtet werden. Den maximalen Fluss erhält man nach Definition des Skalarprodukts bei
zwischen den Funktionsparametern und der Flächennormalen betrachtet werden. Den maximalen Fluss erhält man nach Definition des Skalarprodukts bei  , welches zwei parallelen Vektoren entspricht. Dies korreliert auch mit den Alltagserfahrungen: Wenn das Wasserohr senkrecht gestellt ist, liegen Flussrichtung und Öffnung des Rohres in der selben Richtung und der Wasserdurchsatz wird maximal.
, welches zwei parallelen Vektoren entspricht. Dies korreliert auch mit den Alltagserfahrungen: Wenn das Wasserohr senkrecht gestellt ist, liegen Flussrichtung und Öffnung des Rohres in der selben Richtung und der Wasserdurchsatz wird maximal.
Summiert man alle einzelnen Teilstückchen auf, erhält man die folgende Darstellung des Flächenintegrals:
Allerdings ist dies wiederum nur eine Approximation, daher muss auch hier der Grenzwert gebildet werden, in dem die Teilflächenanzahl gegen unendlich geht, während ihre Flächen infinitesimal klein werden. Aus diesem Grenzwert der Summe entsteht das Oberflächenintegral über die Fläche A, also der Fluss durch diese Fläche. Zur Berechnung des Flächenintegrals verwendet man folgende Form:
Anschließend seien zwei Sonderfälle genannt, die häufig auftreten und den Rechenaufwand verkleinern:
1.Fall
Ist der eingeschlossene Winkel 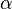 Null, also wenn die beiden Vektoren
Null, also wenn die beiden Vektoren 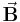 und
und 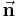 überall parallel sind, dann folgt:
überall parallel sind, dann folgt:
Die Paramater müssen nun nicht mehr als Vektoren angesehen werden.
2.Fall Wenn außerdem B über die ganze Fläche A konstant ist, folgt:
Die Integration geht dann in eine einfache Multiplikation der Flussdichte B mit dem Flächeninhalt A über.
Eine zylinderförmige homogene Raumladung Da die Anordnung unendlich ausgedehnt ist, ist Für das Flächenelement Die elektrische Feldstärke wird nur von dem Radius r bestimmt und sie steht senkrecht auf der Mantelfläche:
Da die eingeschlossene Ladung |
Multimediale Lehrmaterialien
|
http://www.surendranath.org/Applets/Electricity/BSLMFACC/BSL.html Applet zum Darstellen des Magnetischen Feldes http://susannealbers.de/pk_applets/efeld/06wissen-physik-efeld.html Applet zu Punktladung und deren Feldlinien und Potenziale http://www.slu.edu/classes/maymk/banchoff/FluxIntegral.html Applet zur Oberflächenintegration (engl.) http://demonstrations.wolfram.com/DoubleIntegralForVolume/ Applet: Doppelintegral über ein Volumen mit Hilfe von Unter und Obersummen (engl./ free CDF-Player erforderlich) |
Hilfreiche Links
|
http://www.uni-magdeburg.de/exph/mathe_gl/oberflaechenintegral.pdf Bebilderte Beschreibung zu Oberflächenintegralen http://math.intelarts.com/doubint1.htm Bebilderte Erläuterung zum Doppelintegral http://www-hm.ma.tum.de/integration/course/html/ch2/t/t_parent.htm Verschiedene Anwendungen der Integration http://www.uni-magdeburg.de/exph/mathe_gl/oberflaechenintegral2.pdf Detaillierte Beschreibung zum Oberflächenintegral mit Beispielrechnung http://www.hoever.fh-aachen.de/SS06/mathe/skript/Mathe2-2.pdf Erklärung zum mehrdimensionalen Integrieren http://mathworld.wolfram.com/SurfaceIntegral.html Formeln und kurze Erklärung zur Oberflächenintegration (engl.) http://www.ltcconline.net/greenl/courses/117/DoubIntProb/Volume.htm Erklärung zum Doppelintegral (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
| ← Zurück: Das Linienintegral | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Das Volumenintegral → |
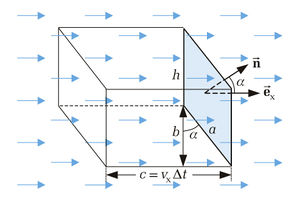
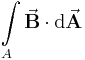
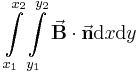
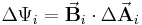
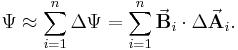
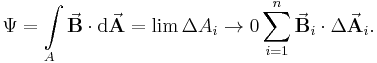
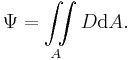
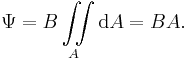
 erstreckt sich idealerweise unendlich lang in eine Raumrichtung. Möchte man nun die Feldstärke berechnen, wählt man den Gausschen Satz:
erstreckt sich idealerweise unendlich lang in eine Raumrichtung. Möchte man nun die Feldstärke berechnen, wählt man den Gausschen Satz:

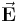 über z überall gleich. Die Raumladung ändert sich auch nicht in Abhängigkeit von
über z überall gleich. Die Raumladung ändert sich auch nicht in Abhängigkeit von  , daher spricht man hier von einer rotationssymetrischen Anordnung. Daraus folgt, dass die elektrische Feldstärke nur vom Radius abhängig ist:
, daher spricht man hier von einer rotationssymetrischen Anordnung. Daraus folgt, dass die elektrische Feldstärke nur vom Radius abhängig ist:

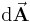 ergibt sich:
ergibt sich:


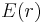 ist nicht von
ist nicht von  abhängig, man kann die Konstante vor das Integral ziehen. Integriert man dann über die Grenzen, erhält man die angegebene Form, die nur noch umgestellt werden muss:
abhängig, man kann die Konstante vor das Integral ziehen. Integriert man dann über die Grenzen, erhält man die angegebene Form, die nur noch umgestellt werden muss:

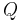 wiederum von der Raumladung und dem eingeschlossenen Volumen abhängt, ist man an dieser Stelle mit der Betrachtung eigentlich noch nicht fertig. Da diese Zusammenhänge in den Übungen auch noch thematisiert werden, und man, wie schon erwähnt, auch das
wiederum von der Raumladung und dem eingeschlossenen Volumen abhängt, ist man an dieser Stelle mit der Betrachtung eigentlich noch nicht fertig. Da diese Zusammenhänge in den Übungen auch noch thematisiert werden, und man, wie schon erwähnt, auch das 
