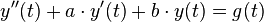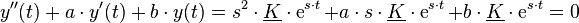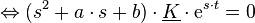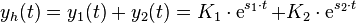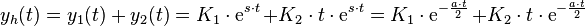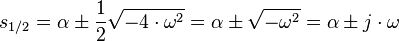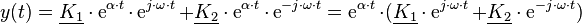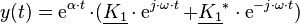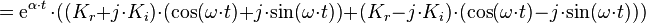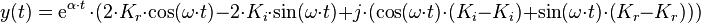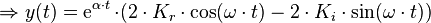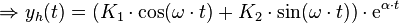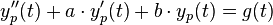Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 2. Ordnung
| ← Zurück: Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 1. Ordnung | Übersicht: Getb:Vorgehen zur Lösung linearer Differenzialgleichungen 2. Ordnung | Vorwärts: Getb:Differenzialgleichungen bei elektrischen Netzwerken → |
Gegeben sei eine inhomogene, lineare Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten. Diese DGL lässt sich allgemein schreiben als:
Wobei 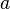 und
und  Konstanten sind. Die Lösung erfolgt genauso wie die Lösung einer DGL 1. Ordnung in vier Schritten:
Konstanten sind. Die Lösung erfolgt genauso wie die Lösung einer DGL 1. Ordnung in vier Schritten:
- Lösung der dazugehörigen homogenen DGL
- Finden einer partikulären Lösung der inhomogenen DGL
- Addieren der beiden Lösungen liefert die allgemeine Lösung der inhomogenen DGL
- Berücksichtigung von Anfangsbedingungen
Inhaltsverzeichnis
Lösung der homogenen linearen Differenzialgleichung
Die zur inhomogenen DGL dazugehörige homogene DGL lautet:
Die allgemeine Lösung einer Differenzialgleichung 2. Ordnung enthält zwei Parameter. Im Falle einer linearen DGL 2. Ordnung mit konstanten Koeffizienten ist die allgemeine Lösung eine Linearkombination von zwei linear unabhängigen partikulären Lösungen. Die Koeffizienten der partikulären Lösungen sind die beiden Parameter. Formal gilt dann für die allgemeine Lösung:
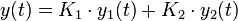 mit
mit 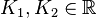 , wobei weiterhin gelten muss:
, wobei weiterhin gelten muss:
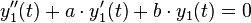 (y1 ist partikuläre Lösung der homogenen DGL)
(y1 ist partikuläre Lösung der homogenen DGL)
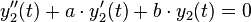 (y2 ist partikuläre Lösung der homogenen DGL)
(y2 ist partikuläre Lösung der homogenen DGL)
-
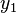 und
und 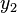 sind linear unabhängig
sind linear unabhängig
Beide Lösungen müssen also die DGL erfüllen und linear unabhängig sein. Allgemein gilt, dass die Lösungen 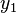 und
und 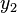 auch komplexwertig sein können.
auch komplexwertig sein können.
Zwei linear unabhängige partikuläre Lösungen lassen sich mit Hilfe des komplexen Exponentialansatzes 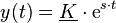 finden. Hierbei ist zu beachten, dass mit
finden. Hierbei ist zu beachten, dass mit 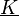 schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem
schon eine Konstante (bzw. ein Parameter) in den Ansatz eingebracht wurde. Der Unterstrich unter dem 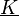 deutet an, dass
deutet an, dass 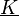 komplexe Werte annehmen kann. Auch die Variable
komplexe Werte annehmen kann. Auch die Variable  kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass
kann komplexe Werte annehmen, wird üblicherweise aber nicht unterstrichen. Für den Fall, dass  komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten
komplexe Werte annimmt, wird der Ausdruck der e-Funktion selbst auch eine komplexe Zahl (vgl. z.B. Papula (2011): „Mathematik für Ingenieure und Naturwissenschaftler“, Bd. 1, Kapitel VII p. 652 ff.). In den meisten Fällen (und auch in der Vorlesung GET B) ist man aber nur an reell wertigen Lösungen für die DGL interessiert, da die gesuchten Ströme oder Spannungen reelle Größen sind. Deshalb ist es notwendig, komplexwertige Konstanten 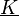 anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann.
anzunehmen. Im weiteren Verlauf wird deutlich, dass dadurch, mit bestimmten Anforderungen an die komplexen Konstanten, eine allgemeine komplexe Lösung auf eine allgemeine reelle Lösung der DGL zurückgeführt werden kann.
Der Exponentialansatz und dessen Ableitungen 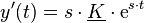 und
und 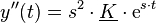 können nun in die homogene DGL eingesetzt werden:
können nun in die homogene DGL eingesetzt werden:
Diese Gleichung ist erfüllt, wenn einer der Faktoren 0 ist. Die e-Funktion kann niemals 0 sein, und der Fall  führt zu der trivialen Lösung
führt zu der trivialen Lösung 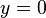 . Somit muss der Ausdruck in der Klammer zu Null werden. Die daraus resultierende Bedingung
. Somit muss der Ausdruck in der Klammer zu Null werden. Die daraus resultierende Bedingung  heißt charakteristische Gleichung und kann zum Beispiel mit der p-q-Formel aufgelöst werden:
heißt charakteristische Gleichung und kann zum Beispiel mit der p-q-Formel aufgelöst werden:
Die Lösungen 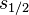 heißen Eigenwerte. Es ergeben sich drei verschiedene Lösungsfälle:
heißen Eigenwerte. Es ergeben sich drei verschiedene Lösungsfälle:
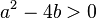 → Die charakteristische Gleichung hat zwei verschiedene, reelle Lösungen
→ Die charakteristische Gleichung hat zwei verschiedene, reelle Lösungen
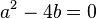 → Die charakteristische Gleichung hat zwei gleiche, reelle Lösungen
→ Die charakteristische Gleichung hat zwei gleiche, reelle Lösungen
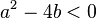 → Die charakteristische Gleichung hat zwei zueinander konjugiert komplexe Lösungen (komplexe Lösungen treten stets als konjugiert komplexe Paare auf)
→ Die charakteristische Gleichung hat zwei zueinander konjugiert komplexe Lösungen (komplexe Lösungen treten stets als konjugiert komplexe Paare auf)
Fall 1 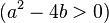
Die beiden voneinander verschiedenen, reellen Eigenwerte 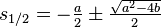 führen mit dem Exponentialansatz auch zu zwei verschiedenen reellen Lösungen der homogenen DGL:
führen mit dem Exponentialansatz auch zu zwei verschiedenen reellen Lösungen der homogenen DGL:
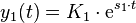 und
und 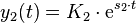 mit
mit 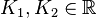
Da die Exponentialfunktionen reell sind, müssen auch die Konstanten 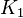 und
und 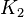 reell sein, damit die resultierende allgemeine Lösung reell ist. Die beiden Lösungen
reell sein, damit die resultierende allgemeine Lösung reell ist. Die beiden Lösungen 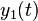 und
und  sind linear unabhängig. Deshalb gilt für die allgemeine Lösung der homogenen DGL 2. Ordnung mit konstanten Koeffizienten, bei der zwei unterschiedliche reelle Eigenwerte auftreten:
sind linear unabhängig. Deshalb gilt für die allgemeine Lösung der homogenen DGL 2. Ordnung mit konstanten Koeffizienten, bei der zwei unterschiedliche reelle Eigenwerte auftreten:
Fall 2 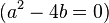
Da die beiden Eigenwerte 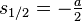 gleich sind, ergibt sich aus dem Exponentialansatz nur eine Lösung:
gleich sind, ergibt sich aus dem Exponentialansatz nur eine Lösung:
 mit
mit 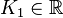
Die Exponentialfunktion ist reell, deshalb muss auch der Parameter 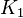 reell sein, da für
reell sein, da für 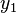 nur reelle Lösungen in Frage kommen. Der Exponentialansatz führt in diesem Fall aber nur zu einer Lösungsfunktion, es werden jedoch zwei linear unabhängige Lösungsfunktionen für die allgemeine Lösung benötigt. Mit dem Verfahren „Variation der Konstanten“ (Idee: Einsetzen der Lösung aus dem Exponentialansatz und Annahme einer veränderlichen Konstante
nur reelle Lösungen in Frage kommen. Der Exponentialansatz führt in diesem Fall aber nur zu einer Lösungsfunktion, es werden jedoch zwei linear unabhängige Lösungsfunktionen für die allgemeine Lösung benötigt. Mit dem Verfahren „Variation der Konstanten“ (Idee: Einsetzen der Lösung aus dem Exponentialansatz und Annahme einer veränderlichen Konstante 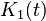 ) lässt sich eine weitere unabhängige Lösung
) lässt sich eine weitere unabhängige Lösung 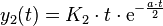 mit
mit 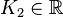 finden. Dass dies tatsächlich eine Lösung der DGL ist, lässt sich durch Einsetzen in die DGL verifizieren. Die allgemeine Lösung für eine homogene DGL 2. Ordnung mit konstanten Koeffizienten, bei der zwei gleiche Eigenwerte auftreten, ergibt sich damit durch:
finden. Dass dies tatsächlich eine Lösung der DGL ist, lässt sich durch Einsetzen in die DGL verifizieren. Die allgemeine Lösung für eine homogene DGL 2. Ordnung mit konstanten Koeffizienten, bei der zwei gleiche Eigenwerte auftreten, ergibt sich damit durch:
Fall 3 
Mit den Abkürzungen 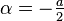 und
und 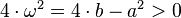 (da
(da 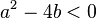 ) lassen sich die Eigenwerte folgendermaßen angeben:
) lassen sich die Eigenwerte folgendermaßen angeben:
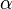 ist also der Realteil und
ist also der Realteil und 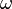 der Imaginärteil der Eigenwerte. Einsetzen der Lösungen in den Exponentialansatz und addieren der beiden Ansätze liefert:
der Imaginärteil der Eigenwerte. Einsetzen der Lösungen in den Exponentialansatz und addieren der beiden Ansätze liefert:
Und weiter umgeformt:
Da nur reelle Lösungen relevant sind, muss zusätzlich gelten, dass die Parameter komplex konjugiert zueinander sein müssen, also  . Dies wird durch Einsetzen des Zusammenhangs und Umformen unter Ausnutzung der Eulerschen Formel deutlich. Mit
. Dies wird durch Einsetzen des Zusammenhangs und Umformen unter Ausnutzung der Eulerschen Formel deutlich. Mit 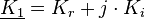 ergibt sich dann:
ergibt sich dann:
Ausmultiplizieren liefert:
Mit den Konstanten 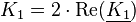 und
und  . Es wurden also die komplexen Konstanten
. Es wurden also die komplexen Konstanten 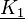 und
und 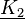 durch die reellen Konstanten
durch die reellen Konstanten 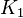 und
und 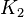 ausgetauscht. Damit wurde die reelle allgemeine Lösung für eine homogene DGL 2. Ordnung mit konstanten Koeffizienten gefunden, bei der zwei komplexe linear unabhängige Lösungsfunktionen und zwei konjugierte komplexe Eigenwerte auftreten.
ausgetauscht. Damit wurde die reelle allgemeine Lösung für eine homogene DGL 2. Ordnung mit konstanten Koeffizienten gefunden, bei der zwei komplexe linear unabhängige Lösungsfunktionen und zwei konjugierte komplexe Eigenwerte auftreten.
Zusammenfassung der drei Fälle
1.Fall: 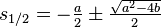 mit
mit 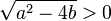 (zwei verschiedene, reelle Eigenwerte).
(zwei verschiedene, reelle Eigenwerte).
Allgemeine Lösung: 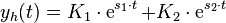
2.Fall: 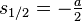 (zwei gleiche, reelle Eigenwerte).
(zwei gleiche, reelle Eigenwerte).
Allgemeine Lösung: 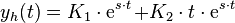
3.Fall: 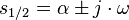 (zwei zueinander konjugiert komplexe Eigenwerte)
(zwei zueinander konjugiert komplexe Eigenwerte)
Allgemeine Lösung: 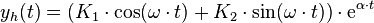
Lösung der inhomogenen Differenzialgleichung
Da nun die allgemeine Lösung der dazugehörigen homogenen DGL bekannt ist, kann eine partikuläre Lösung der inhomogenen DGL gefunden werden, um die allgemeine Lösung der Differenzialgleichung zu erhalten. Diese ergibt sich dann durch Addition beider vorher gefunden Lösungen.
Für eine partikuläre Lösung der inhomogenen DGL muss gelten:
Das Finden einer partikulären Lösung wird besonders einfach, wenn 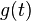 konstant ist. Dann kann für
konstant ist. Dann kann für 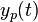 ebenfalls ein konstanter Ausdruck angesetzt werden, dessen Ableitungen 0 sind. Für die allgemeine Lösung der inhomogenen DGL 2. Ordnung ergibt sich dann:
ebenfalls ein konstanter Ausdruck angesetzt werden, dessen Ableitungen 0 sind. Für die allgemeine Lösung der inhomogenen DGL 2. Ordnung ergibt sich dann:
Wobei sich die Form von 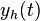 nach der Fallunterscheidung im vorherigen Abschnitt richtet.
nach der Fallunterscheidung im vorherigen Abschnitt richtet.
Anpassung der allgemeinen Lösung an eine spezielle Anwendung
Die allgemeine Lösung einer DGL 2. Ordnung besitzt zwei unbestimmte Konstanten (Parameter). Durch von außen gegebene Anfangswerte ergeben sich konkrete Werte für die Konstanten. Um beide Konstanten zu bestimmen, müssen zwei Anfangsbedingungen eingearbeitet werden. Diese sind von außen vorgegeben, und werden in der Form 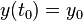 und
und 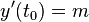 angegeben. Das Einsetzen liefert dann zwei Gleichungen. Sollten in beiden Gleichungen beide Konstanten
angegeben. Das Einsetzen liefert dann zwei Gleichungen. Sollten in beiden Gleichungen beide Konstanten 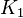 und
und 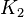 vorkommen, müssen Verfahren der linearen Algebra angewandt werden, um das Gleichungssystem zu lösen (z.B. Einsetzungsverfahren). Mit den bestimmten Konstanten ergibt sich dann die endgültige Lösung für die inhomogene DGL 2. Ordnung.
vorkommen, müssen Verfahren der linearen Algebra angewandt werden, um das Gleichungssystem zu lösen (z.B. Einsetzungsverfahren). Mit den bestimmten Konstanten ergibt sich dann die endgültige Lösung für die inhomogene DGL 2. Ordnung.
Zusammenfassung
Die Lösung einer inhomogenen linearen DGL 2. Ordnung mit konstanten Koeffizienten erfolgt analog zur Lösung einer linearen DGL 1. Ordnung in vier Schritten:
- Lösen der zugehörigen homogenen linearen DGL
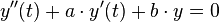 mit Hilfe des komplexen Exponentialansatzes
mit Hilfe des komplexen Exponentialansatzes 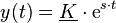 . Das Lösen der charakteristischen Gleichung
. Das Lösen der charakteristischen Gleichung  liefert die Eigenwerte
liefert die Eigenwerte 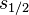 . Abhängig von der Art der Eigenwerte
. Abhängig von der Art der Eigenwerte 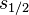 ergibt sich einer von drei verschiedenen allgemeinen Lösungsansätzen für
ergibt sich einer von drei verschiedenen allgemeinen Lösungsansätzen für 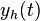 .
. - Finden einer speziellen (partikulären) Lösung
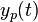 , welche die inhomogene DGL löst.
, welche die inhomogene DGL löst. - Addition der allgemeinen Lösung der homogenen DGL und der partikulären Lösung liefert die allgemeine Lösung für die inhomogene DGL:
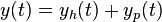
- Eventuelle Anfangsbedingungen
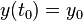 und
und 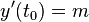 in die allgemeine Lösung, bzw. ihre Ableitung, einsetzen, um die Konstanten
in die allgemeine Lösung, bzw. ihre Ableitung, einsetzen, um die Konstanten 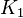 und
und 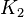 zu bestimmen.
zu bestimmen.